课程思政视域下五年制高职数学项目化学习的实践研究——以《三角计算及其应用》为例
(1泰州机电高等职业技术学校 江苏泰州 225300;2泰州技师学院 江苏泰州 225300)
摘要:在五年制高职数学课程中,以《三角计算及其应用》为例实行项目化学习模式,旨在通过项目化任务引导课堂教学,有机整合数学学科与机电专业学习,解决专业实际问题,并深入挖掘课程思政资源,将思政教育有效融入学生的主体学习活动之中,从而培养学生理性思维的能力、严谨科学的态度及浓厚的家国意识,促进其数学核心素养的培育及价值观的形成。
关键词:课程思政,五年制高职,项目化学习,数学课程
1. 课程思政的发展脉络
“要用好课堂教学这个主渠道,思想政治理论课要坚持在改进中加强,提升思想政治教育亲和力和针对性,满足学生成长发展需求和期待,其他各门课都要守好一段渠、种好责任田,使各类课程与思想政治理论课同向同行,形成协同效应。”这是2016年全国高校思想政治工作会议中的重要论述,为落实“立德树人”根本任务指明了实践方向,是“课程思政”的重要缘起。2018年北京大学师生座谈会中,习总书记进一步指出“要把立德树人内化到大学建设和管理各领域、各方面、各环节,做到以树人为核心,以立德为根本”。这一重要表述促进了“课程思政”的认知不断深入。2018年召开的全国教育大会中进一步明确“要把立德树人融入思想道德教育、文化知识教育、社会实践教育各环节,贯穿基础教育、职业教育、高等教育各领域,学科体系、教学体系、教材体系、管理体系要围绕这个目标来设计,教师要围绕这个目标来教,学生要围绕这个目标来学”,已经表明“课程思政”作为立德树人这一根本任务的重要落实理念和机制的认识基本成型。[1]当下,如何将“课程思政”融入到五年制高职的数学课堂教学中,已然成为了五年制高职数学课程改革面临的一个重要任务。
2. 数学课程思政的的内涵与价值
数学课程作为一门重要的五年制高职公共基础课,在发展学生数学能力与核心素养,培育专业能力等方面发挥着不可替代的独特作用。具体来说,一方面由于具有“高度的抽象性、严密的逻辑性和广泛的应用性”的学科特点,数学课程对培养五年制高职生的数学思维有很重要的作用。另一方面,五年制高职数学课程不仅仅是学生学习专业课程的一项基础应用工具,更是培育学生科学精神,拓展专业综合素质的重要载体,是对学生未来进入工作岗位,融入社会奠定了厚实的素养基础。
数学学科所体现的科学精神与人文精神的融合是实现思想政治教育的重要载体。[2]所以,数学课程思政旨在彰显数学课程的思想政治教育内涵,充分发挥其学科的育人功能,将价值观教育、科学精神及数学文化等思想政治教育元素有机融合数学课程的目标、内容以及实践过程之中。用数学课程丰富的内涵,激发思想政治教育生命力和创造力,进一步深挖其育人价值,拓展其教育教学功能。[3]
3.项目化学习的方法论价值
项目化学习(PBL)源于美国教育家威廉·克伯屈于1918年提出的“设计教学法”,在杜威的实用主义教育哲学和桑代克的学习心理学理论的影响下,经过不断的进步和发展,成为欧美国家学校教育领域盛行的教学方式。在新时代的教育改革浪潮中,项目化学习已经被我国教育工作者所接纳、实践和发展。在当下的职业院校中,专业课程教学更愿意采取项目化的学习方式进行。所以,项目化学习在职业学校具有良好的实践土壤。
项目化学习是一种基于学生为中心的教学模式。在五年制高职的数学课程教学实践中采取项目化学习的模式,可以让学生从真实环境中的基本问题模型出发,围绕较为复杂的且又来自真实专业情境或者生活情境的主题,以小组学习的方式,进行一定学习时段的自主式探究活动,完成一系列包含数学模型构建、数学问题分析与解决、实际问题解决、作品创作以及成果交流等学习任务,并最终实现知识建构、能力提升及素养发展的一种教学模式。
4.基于课程思政的项目选择原则
囿于五年制高职学生的认知基础及学科认知水平较局限,社会生活及生产场景中蕴藏的许多数学知识,并不适合学生在课堂教学环节探究解决。因此,项目的选择需要结合学生的专业特点,围绕学生的生活经验,从数学学科与专业课程交叉的角度进行创设。具体而言,项目的选取和挖掘需要参考以下三个原则:其一,基于课程标准。《五年制高等教育数学课程标准》中明确了五年制高职数学课程的任务,同时要求项目内容源于教材,契合学生的学情特点,从真实的背景中提炼出数学模型,融合专业课程的知识系统,优化项目化任务驱动,培养学生解决实际问题的能力,发展学生数学核心素养。其二,源于生活实践。具象思维是五年制高职学生的重要思维特点,他们对社会热点、自然现象、科学创新等现象表现出极大的好奇和热心,而对较为抽象的原理系统缺乏较为深刻的思辨。因此,项目内容的选择应该从学生生活实践中来,选取学生最为感兴趣的热点事件、自然现象或者技术创新等,将较为抽象、复杂和枯燥的数学原理,通过具象化、生活化的模型或者场景展现给学生,以项目化的学习方式,激发学生的学习热情,促进数学知识与技能的深层次内化。其三,指向价值教育。项目设计的出发点是基于社会真实问题或专业生产实际问题,源于生活真实环境,融合专业应用,具有一定专业实践的综合性。从项目问题的分析、解决方案的设计、实施方案的取舍和总结归纳,以及对解决过程的评价,都与学生的数学学科核心素养培育密不可分。同时在这一过程中,学生也经历了情感、态度及价值观的完整生成过程,特别是在数学学科与专业课程融合学习的过程中,价值观的建立更加牢固,思政教育效果更加深刻。
5.项目化学习的实施过程
项目内容的设计及具体实施是项目化学习的关键,项目的设计一方面基于课程标准,采取分任务设置的方式,逐步突出主题;另一方面围绕学生专业特点及学情基础,明确项目实施中的任务分工和师生协作,突出学生在项目学习中的主体性、积极性以及价值教育的主旨性。在本次项目内容设计和遴选过程中,我们选取学生关注度较高、与学生专业学习经历密切相关的冬奥会开幕式中央舞台系统作为项目研究的主题素材,并将这一素材分为三个小任务模块融合,以期发展学生的数学核心素养,实现课程思政的落地生根。
具体来说,本次项目化学习的教学内容选自马复、王巧林主编的《数学》第四册第十五章《三角计算及其应用》。为了提高学生应用数学思想解决机电专业问题的意识和能力,渗透数形结合思想,在项目设计时适当调整了教材内容,融合机电专业核心课程《机械基础》中的曲柄连杆机构模型为基本专业问题背景,整合《三角计算及其应用》内容为三个项目,共12学时,如表1所示:
表 1
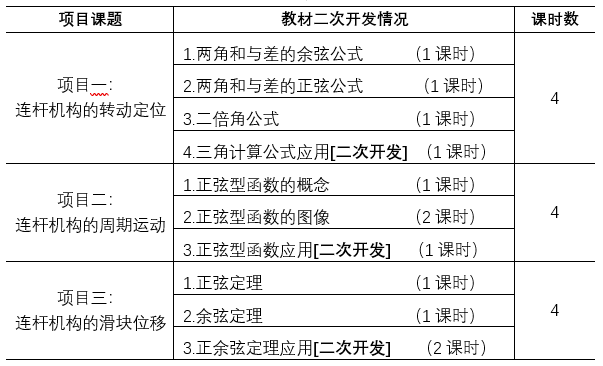
5.1项目的目标任务
本课程授课对象为五年制高职二年级学生,他们已经对三角函数的定义、图像以及性质有了一定的了解,初步具备了应用三角函数知识进行化简、求值的能力。同时以机电专业中连杆机构问题为主线,整合专业课程教学资源,创设教学情境及应用问题,逐步深入数学知识和数学方法的探究与应用。
在学情分析的基础上,结合五年制高职课程标准预设本次项目化学习的目标为:
1.掌握三角计算公式,会根据公式求特殊角的三角函数值,化简三角函数式;
2.经历三角计算公式的推导过程,提高学生推理能力,体会三角变换的思想与方法;
3.通过项目任务的启发,激发学生学习兴趣,在合作学习中增强学习的信心和交流互动的情感;通过公式间互化的推导以及解决简单的专业问题。
5.2项目的组织保障
在《三角计算及其应用》的学习过程中,借助与信息技术可以将复杂的三角变换或者繁冗的理论推导直观显现,也可以将实际问题抽象为简明的几何模型,以此培养学生的直观想象和数学建模能力。因此,在教学过程中,利用泛雅学习平台、腾讯课堂等搭建课前、课中、课后的混合学习模式;利用GGB软件演示专业问题情境,以及显现数学原理的推导过程,从而有效激发学生学习数学的积极性,提高学生的学习能力。在充分的学情分析的基础上,对学生进行合理分组与分工,是进行项目化学习的实施基础保障,一般以3-5人为一个学习小组。在组内根据学生组织领导能力、沟通协调能力以及学习研究能力等分配组内工作角色,指定项目学习计划,逐步完成项目学习任务。
5.3项目的方案设计
依据各个项目学习的任务目标,设计项目学习内容,同时也要考虑学生实践的可行性与师生互动性,有利于学生发挥团队智慧,体验集体学习的乐趣,并不断完善学习计划,达到发展数学核心素养的目的。
下面以项目一“连杆机构的转动定位问题”为例具体说明项目的设计方案及其思政元素的建设情况。
5.3.1创设情境简介
2022年1月4日,北京冬奥组委会按照工作计划将对鸟巢体育馆的中央舞台系统进行一次联合测试,届时将对所有涉及的设备进行高强度检测,以确保即将到来的全员彩排能顺利进行。
5.3.2专业问题情境
在中央舞台系统的升降机测试中,连杆机构的转盘部分发生了一次机械故障。当转盘按照工作指令开始逆时针匀速旋转时,曲柄绕中心同步旋转运动。突然转盘动力系统发生意外故障,导致转盘及曲柄骤停,为了完成既定的测试任务,以便于记录升降机的各部分工作位置,工程师决定通过需要手动操作,将曲柄人工转动到预定位置。
5.3.3问题解决与活动指导
(1)如图1,若将转盘曲柄末端的启动位置记为Q点,曲柄长度r=1,曲柄末端从Q点运动到P_1位置时突然停止运动,此时曲柄已经旋转的角度记为α,请帮助工程师确定P_1位置的坐标;
(2)工程师通过手动操作将曲柄人工转动到预定位置P_2,已知cosα=(-2)/3,∠P_1 OP_2=π/4,请协助工程师确定P_2位置的横坐标;
(3)在曲柄末端到达P_2位置后,如图2,工程师决定将再次启动机构,将转盘反向旋转运动到检修位置P_3,以进行故障检修,若∠P_1 OP_3=π/3,请协助工程师确定P_3位置的横坐标。
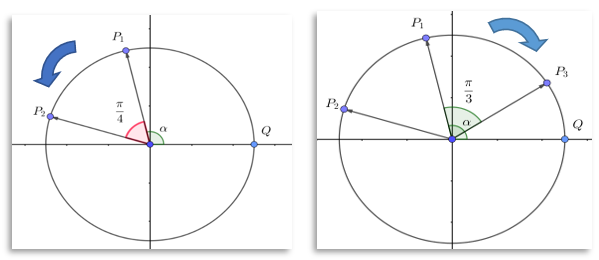
图1 图2
5.3.4课程思政内容建设情况
(1)从社会热点时事中挖掘思政元素。以冬奥会开幕式为话题引入学习,学生在课前收集学习资料,发现祖国在新时代建设取得的巨大成就,内心激起剧烈的爱国情感,能迁移到对专业学习的坚定认同,感受到数学学科对国家建设、民族复兴的巨大作用,从而建立强烈的文化自信、制度自信、道路自信,生成对祖国强烈的热爱之情。
(2)从专业应用领域中深挖思政元素。在学生分析曲柄连杆机构的工作原理并进行数学建模环节中,播放中国航天科学家与工程师合作进行技术攻关的纪录片,让学生了解他们运用创新技术服务于冬奥会的舞台系统设计,创新的向世界传达了中国声音,诉说着中国故事,培育家国意识,树立爱国情怀、歌颂自强不息的精神。
(3)从信息化学习技术层面解析思政元素。借助于信息技术将复杂的三角变换或者繁冗的理论推导直观显现,也可以将实际问题抽象为简明的几何模型,以此培养学生的直观想象和数学建模能力。在此过程中, 教师可以借助软件的演示顺势引出“现象与本质”的辩证关系。因为三角变换具有复杂多样性的“现象”,而其“本质”反映的是三角形的边与角的朴素关系。
(4)从数学知识传授层面引出思政元素。在探究和运用两角和与差的正余弦公式时,学生容易在根据角的范围讨论正弦值的符号问题中产生错误,教师可以引导学生明确角的终边所在象限,依此确定正弦值的符号,并进一步鼓励学生进行正逆向的探究性学习。据此让学生感受重视细节,培养学生严谨细致的科学态度和精益求精的工匠精神。同样在通过等量代换推导两角差的正弦公式时,教师可以引导学生把公式的转化比作社会的丰富多彩,学生要学会保持一颗“等量的”恒心,坚持内心的信仰,树立远大的理想和正确的价值观,终能在社会大潮中实现自己的人生价值。
6.项目化学习模式下课程思政的价值优势
首先,项目化学习模式可以从数学与专业学科融合之中挖掘课程思政元素。无论是数学的学科属性还是与专业课程的关联度,都不能忽视数学对科技进步和对社会发展的巨大推动作用。[4]这些密切的关联以显性或者隐性的方式在数学课程中存在,项目化的学习模式可以通过学生的自主学生、师生的互动合作等方式深入的挖掘,而且根据不同的专业的特色,这种关联性的显现方式会有较大的差别。这也是项目化学习模式的魅力,亟待数学课程的一线教师进一步挖掘。所以,课程思政元素在数学课程的建设可以通过项目化学习模式得到深度的挖掘。
其次,项目化学习模式可以将数学课程中理性思维观自然地植根在学生的观念结构中。项目化学习模式重视数学知识的构建、运用,以及与专业课程的交叉学习。所以,数学在特定的公理系统基础上演绎出的理论体系和思维方式,在项目化学习方式中完整的展现在学生面前。这样的思维方式对于学生辨析社会现象,形成正确的价值判断,树立符合社会主义核心价值观的价值观念具有积极作用,并且这样的思维方式一旦形成,对学生生命成长的指导作用将是终身的。[5]
最后,项目化学习模式有助于学生职业综合素质的培育。从项目化学习模式的实施层面看,学生是整个教学过程的主体。从项目任务的开始,学生就在充分发挥自身的合作动能,在生生合作、师生互动中发展自身的数学核心素养。而这一过程中,学生的综合职业能力也在应用数学解决专业问题中得到体现,所以在专业人才培养的目标的视野下,课程思政的落脚点与学生职业素养的成长在数学课程中找到的共振点。
因此,项目化学习模式中数学课程与专业课程的融合促成了课程思政的课堂落实。在项目化学习的模式之下,课程思政有机的融入到项目的各个环节,从数学基础知识的探究到专业问题背景的解析,从数学模型的构建到专业实际问题的解决都可以巧妙地链接到思政资源。而学生对于在项目学习中的思政元素更能接纳,进而引发思考、激发共鸣。基于项目化的学习模式,在课程思政真正落实到课堂教学中的实践还需要进一步探索和充实,同时也为五年制高职数学课程教学改革添砖加瓦。
参考文献
[1]韩宪洲.课程思政的发展历程、基本现状与实践反思[J].中国高等教育,2021,No.681(23):20-22.
[2]张凯,段妩迪,辛海燕.课程思政研究综述[J].职业技术,2021,20(04):1-6.
[3]徐瑾.课程思政有效融入课堂教学的实践研究——以五年制高职数学课程为例[J].江苏教育研究,2020,No.440,No.441(Z3):20-23.
[4]曹广福.数学课程思政:内涵、目标与实施[J].教育研究与评论(中学教育教学) ,2022,No.495(01):5-9.
[5]杨明全.核心素养时代的项目式学习:内涵重塑与价值重建[J].课程.教材.教法,2021,41(02):57-63.
