初中数学教学中数形结合思想的应用
摘要:若教师能够在开展课堂教学活动过程中对数形结合思想加以充分运用,课堂教学将会取得更加理想的效果,一方面数形结合思想能够有效降低学生的数学知识学习难度,另一方面其对帮助学生灵活运用所掌握的知识也有着诸多裨益。基于此,文章从引入图形、加强讲解方面出发,针对初中数学教师该如何在教学当中有效应用数形结合思想展开探讨。
关键词:初中;数学;数形结合
作者简介:叶红,江苏省南京求真中学教师,研究方向为课程改革。(江苏 南京 210009)
中图分类号:G633.6 文献标识码:A 文章编号:1671-0568(2021)00-0000-00
数形结合思想指将抽象化的数学语言、数量关系与直观的几何图形、位置关系相结合,促使复杂问题简单化、抽象问题具体化,从而令学生能够寻找到最优解题途径的思想。相关调查结果显示,我国目前近六成教师仅仅会偶尔在课堂教学当中提及数形结合这一数学思想,在课堂中经常提及数形结合思想的教师仅占三成,由此不难看出,数形结合思想在我国现阶段初中数学学科教学当中并未得到广泛应用。在实际教学中,部分初中数学教师往往对于理论过于重视,将大部分课堂时间用于推导公式以及为学生提供解题思路等,虽然在必要时会将数与图形相结合,但是并未向学生渗透数形结合思想。这不仅会使学生对数量关系与空间形式难以形成明确认知,也会对其日后使用数学知识灵活解决所遇到的问题造成极大制约,最终对其数学核心素养的形成造成严重影响,因此,在日常课堂教学当中,初中数学教师需对数形结合思想加以充分运用,在促进课堂教学质量提升的同时,为学生的数学思维发展打下良好基础。
一、引入图形
教师若想有效应用数形结合思想,首先便需在课堂知识点教学当中切实做到数形结合,从而帮助学生更为高效与透彻地理解新学的知识点,并且,在讲解过程当中,教师自身也需对图形加以认真分析,促使学生在对数学公式与理论知识形成更深层次理解的同时,对图形形成深刻记忆,令学生在提及相关知识点时能够在脑海中浮现相应图形。例如,在教学一元一次方程时,教师可将一元一次方程比喻成一条直线,斜率越大的直线其倾斜程度也不断增加,而一元二次方程则可比喻成抛物线。又如,在开展“平面直角坐标”教学时,教师可利用图形将直角坐标更加直观地向学生展示(见图1),随后令学生对直角坐标进行观察,并让其以自己的方式讲解直角坐标的基本性质。但是由于直角坐标在平面当中能够无限延伸,所以教师若仅仅依靠图形进行教学难以令学生学习到完整知识,故而在这一过程中,教师还需依靠平行线性质对直角坐标进行判定,以促使学生对平面直角坐标相关知识形成更深层次理解,最终使其完全不需要传统死记硬背方式便能够有效掌握相关知识点。另外,数形结合有助于学生在记忆模糊时通过画图方式总结所学知识点,减少错误率,并实现对所学知识的长久记忆。除此之外,图形在统计学当中也必不可少,其能帮助学生对统计结果做出更加精准的分析有。
图1 平面直角坐标
在教学过程中,教师也可通过平方差公式展开数形结合教学,平方差公式的主要内容为:(a+b)(a-b)=a*a-ab+ab-b*b=a2-b2。教师可以利用数形结合方式更加清楚地向学生展示平方差公式的推导过程(见图2),而不要使用传统枯燥乏味的教学方式实施灌输式教育,以规避教师讲解难、学生学习吃力这一情况。同时,教师也可通过数形结合发散学生的思维,让其根据平方差公式推导过程,结合数形结合思想推算完全平方公式(推导过程见图3),这样教学不仅有利于发展学生的数学思维,还有利于节省课堂教学时间。
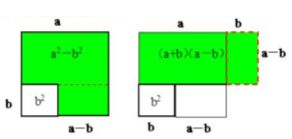
图2 平方差公式推导图
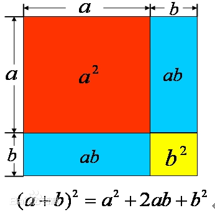
图3 完全平方公式推导图
通过上述举例不难看出,数形结合思想能够帮助学生突破传统学习方式的束缚,由被动接受知识转变为主动接触知识,学生的这一转变能促进师生的有效沟通,也能令数学课堂教学取得更好的效果。
二、加强讲解
初中数学知识具有抽象、逻辑性较强等显著特征,这导致学生的初中数学学习难度加大。因此,在数形结合教学中,教师有必要进行详细讲解,以降低学生的学习难度,并确保学生能够通过学习形成举一反三思维。以一次函数中的一元二次方程教学为例,部分学生在对一次函数相关题目进行解题过程中往往会遇到诸多问题,此时教师便可通过数形结合方式对相关问题进行讲解。首先,教师可将一元二次方程比喻成一条抛物线,并设置问题:一元二次方程公式为:y=ax2+bx+c。其中,a并不等于0,求a、b、c的正负。随后,教师给出图形(见图4、5)并让学生结合图形进行思考。当学生完成解题后,教师可作出解析:a点的正负片段主要取决于抛物线的开口方向,若a>0,表明开口向下,而a<0,则代表抛物线开口向下,首先通过图形可以看出抛物线开口向下,因此得出a<0;b的正负主要取决于抛物线顶点处于第几象限之中,若在第一象限当中,则b>0,若处于第四象限,便<0,由图形可知,抛物线顶点在第一象限当中,因此得出b>0;而要判断c的正负,则完全可以将x=0完全带入至抛物线方程y=ax2+bx+c当中,观察(0,e)坐标与y轴的交接点,若y轴与正半轴相交,则c>0,反之,则c<0。由图形可知,当x=0时,抛物线便是y=c,此时y轴与a点相交,得出c>0。由此可得出结论:a<0,b>0,c>0。

图4 y=ax2+bx+c图像(a>0) 图5 y=ax2+bx+c图像(a<0)
另外,以勾股定理这一知识点为例,这一知识点一直是初中数学教学的难点,教师若想有效降低学习难度,帮助学生更好地运用勾股定理,可通过多媒体将勾股定理图直观展示在学生眼前(见图6),并在展示过程中对勾股定理如何形成进行讲解,当学生对勾股定理相关内容形成一定了解后,教师便可使用不同图形帮助学生有效论证勾股定理,同时也可对《几何原本》中的相关知识内容进行挑选利用,为学生进行更多关于勾股定理如何运用的讲解。这样既能为学生认知与理解勾股定理知识点提供有效帮助,又能够令初中数学教学内容得到大幅度拓展,同时可以为学生在日后日常生活当中灵活运用勾股定理打下良好的基础。
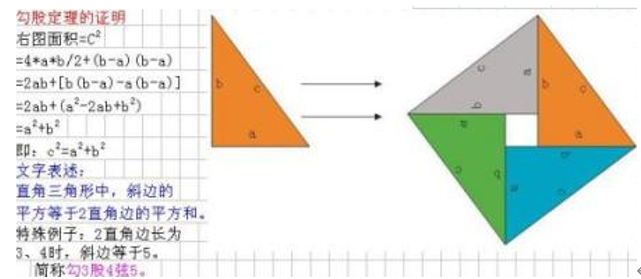
图6 勾股定理证明图
综上所述,由于初中数学具有复杂、抽象等特点,大部分学生难以理解所学知识点,对于这一问题,教师可在初中数学课堂教学活动当中对数形结合思想进行有效运用,因为数形结合思想能帮助学生降低知识学习难度,并且对于促使学生形成数学素养也有着极为良好的促进作用。
参考文献:
[1] 郭礼军.数形结合思想在初中数学教学中的应用[J].数理化解题研究,2021,(8).
[2] 王璠.初中数学教学中数形结合思想的应用[J].读写算,2021,(7).
