机械臂路径特征点目标轨迹规划及实验分析
江苏联合职业技术学院,淮安生物工程分院,江苏淮安 223200
摘要:采用传统机械臂轨迹规划算法存在控制精度不高以及时延较大的问题。为了提高机械臂跟踪目标轨迹效率,设计了一种基于路径特征点算法的机械臂跟踪目标轨迹优化方法。利用相平面法调节使算法达到更高处理效率。研究结果表明:随着路径点数量增加,算法时间明显延长,设置太多路径点可以实现算法效率的显著提升,整个计算过程所需的规划时间能够大幅缩短。采用本文算法可以获得比其它路径规划算法更短的耗时,且更适合于复杂路径。该研究具有很好的实际应用价值,易于推广开来。
关键词:机器臂;路径特征点;时间近似最优;轨迹规划
中图分类号:TP242
Trajectory optimization of manipulator tracking target based on path feature point algorithm
Zhang Qin
Huai ’an Bioengineering Branch, Jiangsu United Vocational and Technical College, Huai ’an 223200, China
Abstract: The traditional trajectory planning algorithm of manipulator has the problems of low control accuracy and large delay. In order to improve the tracking efficiency of manipulator, an optimization method of tracking target trajectory based on path feature point algorithm was designed. The phase plane method is used to adjust the algorithm to achieve higher processing efficiency. The results show that with the increase of the number of waypoints, the algorithm time is significantly extended. Setting too many waypoints can significantly improve the algorithm efficiency, and the planning time required by the whole calculation process can be significantly shortened. The proposed algorithm is shorter in time than other path planning algorithms and is more suitable for complex paths. This research has good practical application value and is easy to be popularized.
Key words: robot arm; Path feature point; time approximation optimal; trajectory planning
1 引言
在移动机器人的运动规划中,机器人往往是以一个点存在,对移动机器人的规划,更多的是使用各种搜索算法,在已经构建好的地图模型上,搜索出一条路径从起始点到终止点的路径曲线。采用传统轨迹规划算法进行分析时只考虑机械臂动力控制过程的非线性特征与电机转速的制约,按照这一方式导致规划轨迹无法完全发挥出机械臂应有的控制性能[1-2]。
现阶段,可以对机械臂动力学模型进行轨迹规划的算法通常选择相平面法,设置路径参数后,再转换机械臂运动学与动力学模型参数能[3]。通过对路径参数进行二阶微分计算构建路径参数化的动力仿真模型,之后建立路径参数模型,使关节速率与力矩约束条件转换成路径约束条件,从而可以利用路径参数二维优化的方式来转换轨迹规划过程能[4-5]。刘学成[6]根据失稳度指标构建得到由模糊神经网络与PID算法共同调节的模型来达到车辆稳定操纵的效果。通过仿真测试可知,采用本文控制方案可以促进车辆操纵稳定性的显著提升。
本文为了提高机械臂跟踪目标轨迹效率,设计了一种基于路径特征点算法的机械臂跟踪目标轨迹优化方法。选择相平面法设置速度曲线,利用相平面法调节的方式使算法达到更高处理效率。
2 路径特征点算法
当设置位姿向量的序列太小时则无法全面保留目标轨迹,造成一定程度的失真能[7-8]。因此根据目标轨迹路径复杂性和动力学模型来提取获得目标轨迹路径参数,进行路径参数计算时则通过模糊推理的方式完成,按照等间距的条件得到路径特征参数。
本实验中设定s=1以及s¨=1,结合虚功计算规则确定惯性力向量,计算式如下:
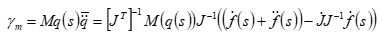
式中,M(q)为机械臂惯性矩阵;q为机械臂关节向量;J(q)为雅可比矩阵;f为路径参数s与机械臂末端位姿p的映射函数。
建立重力加速度向量如下:
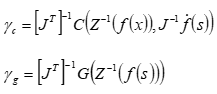
式中,Z为机械臂运动学正解运算。
3 实验
3.1 实验方案
本实验选择可以实现六自由度控制的攻角机械臂作为测试对象测定了轨迹规划算法处理效率与可靠性。图1为机械臂的具体结构,表1给出了不同自由度下对应的力矩/电流与速度约束条件。
PC系统通过人机交互界面软件进行运行状态监控时设置了MATLAB接口来实现轨迹调用[9]。通过工控机调节机械臂软件程序实现动作控制功能,可以精确调节机械臂位置参数并采集关节速度、电流等信息[10]。在工控机中运行机械臂软件,实现位置与速度的调节并使其到达指定部位,同时采集获得电流、速率参数。
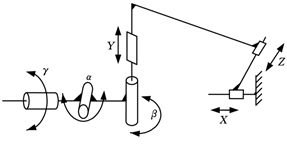
图1机械臂结构示意图
表1关节约束表
参数 X Y Z α β γ
输出电流限制(A) 24 48
速度限制(mm/s)或(°/s) 225 30
3.2 算法有效性
不同时间下的机械臂自由度关节位置变化结果见图2所示.由图2可以看到此时形成了与预期相符的连续分布关节位置曲线,使机械臂与所有关节时间序列形成精确跟踪的状态,可以有效实现机械臂驱动功能。机械臂保持紧密跟踪状态,X自由度驱动电流与额定电流的边界参数相近,其余自由度都比额定电流边界更低[11]。
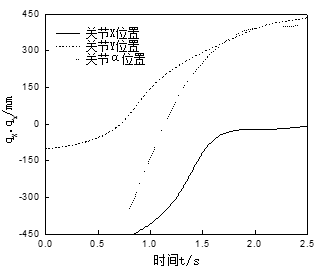
图2关节位置曲线
3.3 算法计算效率分析
3.3.1路径特征点数目优化
没有选择路径特征点算法的条件下,由路径特征点组成序列集,同时受到路径的复杂性与机械臂的非线性结构影响[12]。特征点算法时来规划复杂目标轨迹时所需的计算耗时结果见图2所示。由图2可知,随着路径点数量增加后,会导致算法时间的明显延长,设置太多路径点数量的条件下以路径特征点算法处理时可以实现算法效率的显著提升。
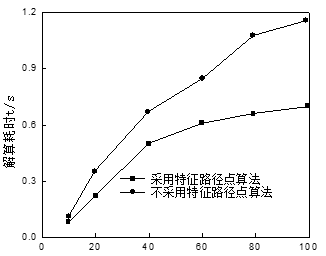
图9 算法效率统计
轨迹规划算法计算时间统计结果见表2所示。对表2结果进行分析可以发现,未优化的条件下采集得到的多重约束最大速度曲线占用了最大比例的处理时间,尤其是处理复杂目标轨迹规划时相对简单目标轨迹需要占用更长时间。经过优化处理后,多重约束最大速度曲线时间明显缩短。以上结果表明,以加速度为0的速度曲线取代多重曲线时,整个计算过程所需的规划时间能够大幅缩短。
表2轨迹规划算法计算时间/%
目标轨迹 T1 T2 T3
优化前简单 21.62 79.63 0.26
优化前复杂 8.06 88.94 0.29
优化后简单 45.78 52.63 5.86
优化后复杂 41.15 56.42 4.68
3.3.2算法对比
以遗传算法作为对比对象,测试了简单与复杂轨迹处理效率,计算效率结果见表3所示。由表3可以看到,采用本文设计的轨迹规划算法可以获得比其它路径规划算法更短的耗时,而遗传算法消耗了最长的时间。
表3计算效率结果对比
参数 路径点算法 遗传算法
简单目标轨迹 0.415 3.462
复杂目标轨迹 0.598 6.896
曲线规划算法具备比遗传优化算法与遗传算法更快处理效率,同时也受到路径复杂性的直接影响,随着路径复杂度的提高,需要消耗更长的规划时间;路径点数量则是规划算法的一个最关键影响因素,当路径点太多时将会造成轨迹规划效率的下降。
4 结论
本文设计了一种基于路径特征点算法的机械臂跟踪目标轨迹优化方法,研究得到如下有益结果:
1)随着路径点数量增加,算法时间明显延长,设置太多路径点可以实现算法效率的显著提升,整个计算过程所需的规划时间能够大幅缩短。
2)采用本文算法可以获得比其它路径规划算法更短的耗时,且更适合于复杂路径。
参考文献:
[1]张鸿儒, 王志刚, 郭宇飞. 振动基柔顺弹药传输机械臂的鲁棒跟踪控制[J]. 机械设计与制造, 2022(07): 149-154+158.
[2]丛明, 宋宏祥, 刘冬, 等. 基于改进珊瑚礁算法的机械臂快速逆解分析[J]. 组合机床与自动化加工技术, 2022(06): 14-18.
[3]张振, 李新宇, 董昊臻, 等. 基于约束采样RRT的机械臂运动规划[J]. 计算机集成制造系统, 2022, 28(06): 1616-1626.
[4]孙颙琰, 郭文勇, 孙云岭, 等. 基于自适应变换蝙蝠算法的机械臂轨迹优化[J]. 机械传动, 2022, 46(05): 35-41.
[5]谢啸, 张涵, 汤自林, 等. 基于动态系统稳定估计器的机器人变刚度轨迹规划[J]. 中南大学学报(自然科学版), 2022, 53(04): 1250-1258.
[6]刘学成, 刘俊, 李汉杰. 基于相平面法的车辆直接横摆力矩控制研究[J]. 合肥工业大学学报(自然科学版), 2019, 42(11): 1455-1461.
[7]孙晓军, 宋代平, 林敬周, 等. 风洞上攻角机器人轨迹规划算法研究与实现[J]. 中国机械工程, 2021, 32(16): 1963-1971.
[8]薛明, 许德刚. 基于云网格集成调度的防拥堵车辆路径规划算法[J]. 计算机科学, 2015, 42(07): 295-299.
[9]屈海军, 杨森. 基于二型模糊遗传控制器的冗余自由度机械臂运动控制的研究[J]. 中国工程机械学报, 2021, 19(02): 117-122.
[10]刘学成, 刘俊, 李汉杰. 基于相平面法的车辆直接横摆力矩控制研究[J]. 合肥工业大学学报(自然科学版), 2019, 42(11): 1455-1461.
[11]李秀智, 彭小彬, 方会敏, 等. 基于RANSAC算法的植保机器人导航路径检测[J]. 农业机械学报, 2020, 51(09): 40-46.
[12]张凤, 孙哲, 孟彬. 一种基于特征点的移动机器人路径规划算法[J]. 沈阳建筑大学学报(自然科学版), 2009, 25(06):1212-1216.
作者简介:张钦,江苏淮安人,男,1987-,硕士学位,研究方向机电控制,工业机器人。13915100162,邮编223200。
