一元线性回归问题的可视化教学案例研究——基于GeoGebra平台
摘 要:本文研究了一元线性回归问题的可视化教学案例。基于GeoGebra平台,通过一个具体的实际教学案例研究不同函数模型拟合效果、函数拟合的残差比较等,实现一元线性回归问题的教学可视化,并在与传统教学设计对比后得出可视化教学具有有效增强教学效果、提高学生学习积极性的结论。
关键词:教学设计;GeoGebra;可视化;
对于初识统计学问题的职业学校学生来说,回归分析问题的学习对初等函数知识要求较高的,且具有计算量较大,思维抽象的特点。GeoGebra是一款动态数学软件,同时具备代数变量运算、统计概率以及2/3D绘图等实用功能[1]。GeoGebra软件通过便捷计算代数系统和智能指令输入系统,真正实现了数与形的融合,将抽象的数据关系可视化为可具体感知的图像信息,激发中职生数学的学习兴趣,提升学生数学核心素养[2]。
1.教材解读
1.1教学目标与教学重难点
《一元线性回归》是江苏职业学校文化基础课《数学》第十章第八节的内容。其教学的重点是了解一元线性回归的基本思想与方法,难点是理解回归模型建立的基本步骤。
1.2传统教学设计流程
茶水销售问题:商店为了解茶水销售量与最低气温之间的关系,随机统计并制作了某六天的销售量(单位:杯)与当天最低气温(单位:oC)的对照表1.
表1
最低气温 26 18 13 10 4 1
茶水销售量 20 24 34 38 50 64
若某一天最低气温为-5 oC,能否估计这天商店卖出茶水的杯数?
在教材中,以此题作为引入问题,要求建立茶水销量y关于气温x的一元线性回归方程。从传统教学设计的角度,此题包括了以下三个问题的讨论与解决:(1)作出热茶销售量与气温的散点图,根据散点图建立它们间的函数关系:(2)建立以温度为自变量,茶水销售杯数为因变量的一元线性回归模型,计算残差并利用残差进行数据分析;(3)计算W(a,b),并利用最小二乘法对建立的模型进行分析,判断能否较好的刻画温度和销售量间的数量关系,最终生成一元线性回归方程。
2.基于GeoGebra平台的教学过程
GeoGebra软件具有数据统计与分析、函数绘图和强大的代数运算功能,故我们利用GeoGebra软件,针对该课题实施教学活动。
2.1建立一元线性回归模型环节
2.1.1绘制散点图
启动GeoGebra软件后,在主菜单栏中的“视图”选项里单击“表格区”,则在界面右侧弹出表格区。然后,在表格区输入表1中的“最低气温”、“茶水销售量”及对应数量。接着,框选数据,通过右键弹出对话框,选择对话框中的“创建”—“点列”栏目。此时,绘图区内生成数据散点图,即生成点列为l1。
教师在生成散点图后,再呈现教材中的散点图,由学生对两张图片进行对比、分析两张图片的区别,再总结汇报,教师进行点评。学生会发现教材中的坐标系的纵轴已经进行了缩放,散点分布失真。那么,“散点分布的规律到底是满足什么样的特征?”仅仅依靠直观印象是不能做出正确的判断的,由此学生探究的愿望渐浓,期待进行下一步的探究。
2.1.2建立一次函数模型环节
散点图生成后教师指导学生观察其特征,回顾已掌握的函数图像,由学生猜想并尝试建立回归模型。学生在小组讨论后汇报,大部分学生都能得出“散点图分布在一条直线附近”的结论。也会有一部分学生猜想二次函数、幂函数的情况。针对这一情况,教师要及时给予表扬,引导全班首先尝试建立一次函数回归模型,并将其他情况作为拓展任务暂不展开。
首先,教师指导学生在指令栏里输入“多项式拟合”,弹出“多项式拟合(﹤点列1﹥,﹤多项式次数﹥)”指令提示。
接着,将其中“﹤点列1﹥,﹤多项式次数﹥”改为“l1,1”,并点击回车后,此时在绘图区中生成一次函数图像f(x),同时在代数区内显示函数f(x)=-1.71x+58.86,在计算机生成一次回归函数后,教师则呈现回归直线的数学定义:“用直线方程近似表示的相关关系叫做线性关系,这条直线成为回归直线,其中a,b称为回归系数。学生回答出计算机生成的回归系数为“a=1.71,b=58.86”。
2.1.3一次函数模型残差分析环节
教师指导学生在指令区内输入“残差图”,弹出“残差图(﹤点列﹥,﹤函数﹥)”,将其改为“残差图(l1,f(x))”,则在绘图区内呈现出一次函数模型的残差图。如图1所示的残差图。
在残差图的直观演示下,教师引导学生将残差与方差进行对比,促进学生对残差这一概念的理解。然后,教师再借助残差图,简要介绍残差的平方和表达式以及求解回归系数的最小二乘法。最后,给出一元回归直线的系数计算公式。
2.2回归模型拓展环节
2.2.1建立二次函数、幂函数模型环节
教师依据学生猜想的另外两种回归模型:二次函数与幂函数模型,指导学生自主完成计算机绘图任务。首先,教师指导学生在指令栏里输入“多项式拟合”,弹出“多项式拟合(﹤点列1﹥,﹤多项式次数﹥)”指令提示。接着,将其中“﹤点列1﹥,﹤多项式次数﹥”改为“l1,2”,并点击回车后,此时绘图区中生成二次函数的函数图像g(x),并且代数区内会呈现函数g(x)=0.06x2-3.4 x+65.52。然后,在指令栏里输入“幂函数”,弹出“幂函数拟合(﹤第一象限点列1﹥)”指令提示。接着,将其中“﹤第一象限点列1﹥”改为“l1”,并点击回车后,此时在绘图区中生成幂函数图像h(x),同时在代数区内显示函数h(x)=72.34x-0.35。
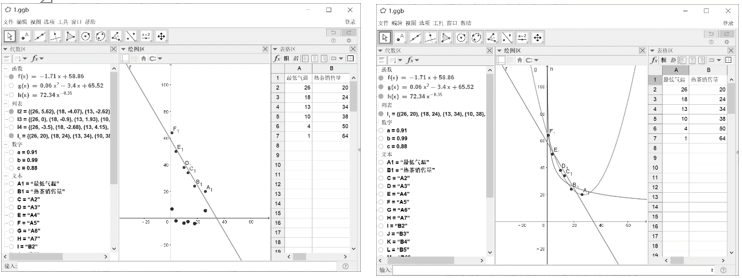
图1 图2
2.2.2不同函数模型拟合效果的比较
教师知道学生作出二次函数与幂函数模型的残差图。通过学生先观察、讨论、再分析比较,发现二次函数模型的残差分布于在x轴附近,残差绝对值也较小;幂函数模型残差在x轴附近分布较为分散,即残差绝对值较大,所以得出结论:二次函数模型拟合较幂函数模型好。但学生也会提出质疑“仅凭直观感知,没有计算”是不能作为充分条件的。
因此,教师顺势指导学生利用R2值验证猜测结论。
首先,在指令栏里输入关键词“可决系数”,提示“可决系数R方(﹤点列1﹥,﹤函数﹥),将其中“﹤点列1﹥,﹤函数﹥”改为“l1,f(x)”,单击回车键后,在代数区内显示a=0.91(即R2=0.91)。
然后,在指令栏里输入关键词“可决系数”,提示“可决系数R方(﹤点列1﹥,﹤函数﹥),将其中“﹤点列1﹥,﹤函数﹥”改为“l1,g(x)”,并单击回车键,在代数区内显示b=0.99(即R2=0.99)。
最后,在指令栏里输入关键词“可决系数”,提示“可决系数R方(﹤点列1﹥,﹤函数﹥),将其中“﹤点列1﹥,﹤函数﹥”改为“l1,h(x)”,再单击回车键,在代数区内显示c=0.88(即R2=0.88),
在对三种函数拟合情况的“可决系数”进行比较分析时,教师可以向学生明确R2越大表示拟合效果越好。
观察函数的图象与相应R2值的大小对比,师生可以发现二次函数模型拟合的效果最佳,经比较甚至比教材中提供的一次函数模型拟合的效果更为精密,但是幂函数模型的拟合效果是三者中最差的。再将三种模型刻画在同一坐标系之中则更具视觉直观性,如图2所示。故而可以借助二次函数解析式对-5 oC的情况预测小卖部卖出茶水的杯数。
3.两种教学设计效果分析
基于GeoGebra软件的教学设计,给课堂教学创设了一个学生大胆猜想,自主探索,即时生成的学习情境。第一,本次课的设计节省了学生手动作图及计算的时间,学生参与思考、交流讨论的意识得到加强。第二,相比传统的教学设计,本次的设计拓展了二次函数与幂函数模型的探究,这产生于GeoGebra软件可视化效果作用下的课堂即时生成。第三,相比较传统教学设计中直接引入残差平方值的计算,GeoGebra软件中残差图的运用更具直观性,有利于学生从直观感知过渡到理性认知,进一步进行针对几种函数模型进行主动地解构与对比。所以,本课题的教学设计中生成的二次函数拟合程度较好的结论,是相对于教材中一次函数模型更加合理的一种函数模型的呈现,是一种机智的教学生成。
参考文献
[1]张志勇.高中数学可视化教学:原则、途径与策略:基于GeoGebra平台[J].数学通报,2018,57(7):21-24,28.
[2]张维忠,唐慧荣.可视化教学内容设计的五大原则[J].电化教育研究,2010(10):99-102.
[3]李红美,王镇国,韦俊楠.面向移动终端课堂互动信息的可视化分析——以高中数学为例[J].现代教育技术,2017,27(02):113-119.
A research on visual teaching cases of linear regression problem
Based on GeoGebra platform
Zhangchi Taizhou Higher Vocational School Of Mechanical & Electrical Technology Taizhou City, Jiangsu Province
Sunxiaoxiao Taizhou Technician college Taizhou City, Jiangsu Province
Abstract: The author constructs and analyses fitting effect diagrams and residual plots of different function models, using GeoGebra platform. Then he makes breakthrough in teaching difficulties through optimized teaching designs, which helps to create situations for the students to explore actively and inspires them to learn maths in an actice way.
Key words: teaching designs; GeoGebra; visual
