改进蚁群算法在移动机器人路径规划中的应用研究
(江苏省盐城技师学院,江苏盐城 224001)
摘要:移动机器人作为智能化发展的重要产物之一,为人们提供扫地、擦地、擦窗户等服务,是人类生活中的得力帮手。虽然此类型机器人可以为人们提供多种服务,但是在移动路径规划上尚存在一定提升空间。为了改善机器人移动路径规划精度,加快路径搜索收敛速度,本文在传统蚁群算法基础上,采用蚂蚁相遇方法,在保留蚂蚁遍历路径记忆能力的同时,对算法路径搜索、路径选择、挥发系数进行改进。经过仿真分析验证改进后,算法收敛性能及路径规划性能得到提升。
关键词:移动机器人;改进蚁群算法;路径规划
中图分类号:TP18;TP242 文献标志码:A
目前,应用比较多的是格栅标识方法,该方法是将机器人的工作环境转化为数学模型,在此模型中识别移动路径,为机器人移动路径的规划奠定了基础。关于路径的规划则是需要使用算法,经过计算分析,确定最优路径。蚁群算法路径搜索和选取的重要手段,被人们用来开发机器人移动路径控制程序。由于以往开发的蚁群算法在机器人路径规划中的应用方案,缺少自适应调整,所以收敛速度偏小,不利于最优移动路径的挖掘。为了弥补这些不足,本文对蚁群算法进行改进,并探究改进后的应用方案。
1 移动机器人路径规划的格栅标识
移动机器人路径规划问题的研究,其核心是全局路径规划,按照类别的不同,可以将这个问题拆分为两部分,其中一部分是机器人移动工作的环境建模,另外一部分为路径规划方法的探究。关于移动工作环境模型的构建,主要是将环境范围转化为能够识别的数学模型,以便更加精准的控制移动路径。格栅法是当前应用比较多的一种环境建模方法,通过创建二维直角坐标系,综合分析机器人外形尺寸、障碍物尺寸,绘制栅格,形成3种不同区域。第一类障碍物格栅,此区域不可以通行;第二类半障碍物格栅,需要详细计算,得到精准移动路径;第三类无障碍格栅,可供行驶。
智能识别中,将第一类和第二类栅格均视为不可通行区域,赋值1,第三类格栅赋值0,从而实现机器人路径规划。在标识过程中,采用直角坐标系方法,为栅格定位,或者采用序号法进行标识。相比之下,后者标识方法简单一些,本研究选择序号标识法,对栅格进行定位。
2 蚁群算法的原理及改进
2.1 蚁群算法的原理
关于路径规划方法的研究,建立在模型创建基础上,需要经过精准计算,确定最优路径。蚁群算法,通过模拟蚂蚁行走路线,计算最佳路径。通常情况下,可以将蚂蚁行走路线看作旅行问题,在有效避开障碍物的前提下,通过计算起点和终点的最短路线,确定最终行进路线。假设蚂蚁行走于i,j两个城市之间,n只随机选择行走路线,经过m个时刻后,计算每一只蚂蚁行走路线长度,同时保存最短路径,将此路径作为最优路径,并更新信息素。其中,信息素主要由两部分组成,其中一部分为蚂蚁行走期间留下的信息素,另外一部分为每一条路径挥发的信息素。假设所有蚂蚁行走轨迹信息素为 ,那么完成一次遍历后,更新信息素的计算公式如下:

上述公式中,k代表城市遍历路径长度;Q代表蚂蚁自身的信息素强度大小; 代表蚂蚁在两个城市之间爬行路径上的信息素浓度; 代表遍历城市后的总路径长度; 代表信息素发挥系数。
从公式(3)的表达形式可以看出,信息素浓度大小在很大程度上取决于优化程度,并且信息素浓度与路径存在负相关关系。当遍历路径比较短的情况下,信息素浓度数值偏大。
2.2 蚁群算法的改进
2.2.1 基于路径搜索的算法改进
算法开启时刻,信息素量大小为0,需要经过一段时间的遍历后才会表现出差异。所以,算法初期信息素并未起到爬行路径引导作用,在搜索路径方面耗费了大量时间。为了弥补蚁群算法在路径搜索方面的不足,本文提出蚂蚁相遇方法。这种方法是将蚂蚁拆分为两组,其中一组放置在起点,另外一组放置在终点,分别从两地出发,向对方地点爬行,当两组蚂蚁在路途中相遇后,蚂蚁各自回到初始位置。与传统的单向自由搜索路径相比,这种路径搜索效率更高一些。假设起点蚂蚁为 ,终点蚂蚁为 ,那么两只蚂蚁相遇就可以用以下公式来表示:
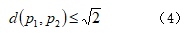
当满足上述条件时,两只蚂蚁在途径相遇,此时两只蚂蚁的路径总长度就是遍历两个城市路径的总长度,记为:
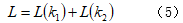
公式(5)中, 代表起点蚂蚁相遇时爬行的最短路径, 代表终点蚂蚁相遇时爬行的最短路径。
2.2.2 基于路径选择的算法改进
依据蚁群算法原理,蚂蚁在爬行过程中路径的选择与信息素浓度大小密切相关,可以将其理解为正反馈机制。如果蚂蚁在爬行过程中在某条路径中留下的信息素较多,则接下来从起点出发的蚂蚁选择此路径的概率就会随之提升。从理论层面分析,这种路径选择方法虽然能够实现智能选择,但是严重限制了蚂蚁爬行路径,缩小了选择空间,很有可能避开最优爬行路径。为了弥补算法在路径选择方面的不足,本文提出扩大搜索范围研究思想,在路径选择设置方面,采取多样性布设,即利用信息素感应进行限定。假设蚂蚁对路径中信息素最小感应数值为 ,当,某条路径的信息素低于 时,则蚂蚁感受不到这个信息素,将选择其他路径。在此情况下,低信息素对蚂蚁爬行路线的影响就会大大降低,使得蚂蚁选择爬行的路径范围得以扩大。
随着算法应用时间的推移,各条路径信息素逐渐增加,当其积累到一定程度后,就会出现大于 的情况,此时信息素开始产生爬行路径引导作用。按照此路径选择方法,可以将蚂蚁在两个城市之间的爬行路径选择概率用以下公式表示:

对于公式(6)阈值范围以外的情况, 。
2.2.3 基于挥发系数调节的算法改进
基于蚁群算法原理,算法性能容易受信息素发挥系数的影响,该系数与蚂蚁爬行路径的引导存在负相关关系,如果系数数值较大,则引导蚂蚁选择爬行路径的作用就会减弱,大大降低了蚂蚁路径选取的智能作用。反之,如果系数数值过小,则引导爬行路径作用加强,导致路径搜索范围减小。为了弥补蚁群算法在发挥系数方面的不足,本文提出一种调整系数的方法,在算法应用初始阶段,适当减小发挥系数数值,使得蚂蚁爬行之间的引导得以下降,达到扩大搜索范围的目的,此时路径搜索效率会随之提升。当路径搜索进入后期时,逐渐增加发挥系数数值,体现群智能选择路径性能,采用此方法快速收敛,从而在短时间内获取最优路径。按照此优化思路,对发挥系数进行调整,计算公式如下:
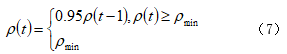
公式(7)中, 代表发挥系数,设定初始值为1。该数值随着算法应用时间的推移,系数数值逐渐减小,最终达到最小值。
3 改进蚁群算法在移动机器人路径规划中的应用
3.1 改进算法的应用
将上述提出的改进蚁群算法应用至移动机器人行走路径规划当中,具体应用流程如下:
第一步:对算法中所有参数采取初始化处理。其中,初始化参数包括 信息素感应阈值、 期望启发因素、 信息启发因子等;第二步:等份分割蚂蚁,将两部分相同数量的蚂蚁分别放置起始点和终点,自适应调整发挥系数,根据不同情况选择爬行路径,直至两组蚂蚁在途径相遇;第三步:每一次遍历后,更新信息素;第四步:统计当前算法循环次数,如果该次数达到了上限,则最后一次生成的最短路径就是最优路径,如果未达到上限,则返回第二步。
3.2 仿真结果分析
为了检验本文提出的改进算法应用方案可靠性,通过仿真模拟分析进行检验。该仿真实验以正方形区域路规划为例,要求机器人从左上角移动到右下角,移动期间避开障碍物。以传统蚁群算法作为对照组,以本文提出的改进算法作为实验组,采用不同算法模拟机器人到达指定地点避开障碍物的行走路径。其中,机器人工作环境中的格栅大小为(20×20),最大迭代次数为300,蚁群规模为30。如图1所示为两种算法遍历期间最大迭代次数仿真结果,图2为两种算法蚂蚁爬行路径规划结果。
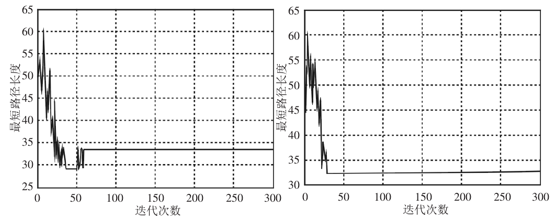
(a)传统算法最大迭代次数变化曲线;(b)改进后的算法最大迭代次数变化曲线
图1两种算法遍历期间最大迭代次数仿真结果
注释:纵坐标以格栅网格数量表示最短路径长度;横坐标为迭代次数,单位:次。
图1中,改进后的算法找到最短路径耗费时间相对短一些,最大迭代次数大约30次,而传统算法的最大迭代次数超过了50次。所以,改进后的算法在收敛速度方面具有一定优势。
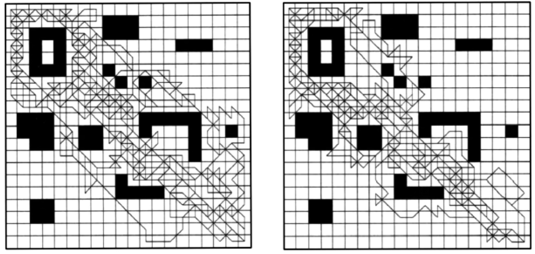
(a)传统算法路径规划结果 (b)改进后的算法路径规划结果
图2两种算法蚂蚁爬行路径规划结果
图2中,与传统算法相比,改进后的算法形成的路径规划效果图覆盖面更小一些,每一条路径与障碍物的距离较小,并且成功避开了更多的障碍物,提高了最优路径遍历精度,有助于机器人快速准确移动到目的地。
4 结束语
本文基于蚁群算法原理,引入蚂蚁相遇策略,改进蚁群算法,并将其应用至机器人移动路径规划当中,通过开展仿真实验,检验算法改进及应用方案可行性。仿真实验结果表明,本文提出的蚁群算法改进方案,不仅保留了蚂蚁种群对爬行路径的记忆能力,以更新后最优遍历路径作为记忆信息,扩大了蚂蚁路径选择范围,加快了算法收敛速度,使得路径搜索效率得以提升。
参考文献
[1]李笑勉,左大利,舒雨锋,等.改进IACA-GM算法在移动机器人路径规划中的研究[J]. 机械设计与制造,2020(12):263-265,271.
[2]赵春芳,李江昊,张大伟.基于改进免疫遗传优化蚁群算法的移动机器人路径寻优研究[J]. 计量学报,2019,40(3):155-160.
[3]涂亮杰,李林升,林国湘.基于改进蚁群算法的果园移动机器人路径规划研究[J].机床与液压,2019,47(23):69-73.
作者简介:董武连(1991-),男,江苏盐城人,本科,高级技师,主要从事实习指导教师、机器人实习、电气安装实习等。
