基于切削用量的机加工成本优化
摘要:在竞争日益激烈的社会大环境下,降低成本成了每个企业必须面对的话题。对于一个从事机械加工的工厂而言,机加工成本的降低则是实现利润最大化尤其重要的一环。文章结合本人工作经历,对机加工成本的影响因素进行了分析概述,并以切削用量中的切削线速度和进给量为切入点,结合刀具的磨损使用情况,阐述了机加工成本降低的可能性和具体分析方法,为工厂的机加工成本优化提供了一种参考。
关键词:机加工;切削用量;成本降低;刀具磨损
1 机加工成本影响因素
对一个从事机械加工的工厂而言,总的生产成本主要来自于三个方面:1)机床成本;2)工装、刀具成本;3)人工成本。其中,人工成本一般是由社会综合因素决定,是不可随意变动的,因此不列入成本优化的考虑范围。工装成本往往是一次性的成本投入,对已经确定的工艺路线,基本起不到成本优化作用。所以,对于机加工成本而言,控制成本就是控制机床成本和刀具成本。
加工一个零件的某道工序,其可控成本是机床成本和刀具成本的总和。对于已经选定的机床来说,机床成本就只取决于机床的纯切削时间和运行效率了。刀具成本取决于刀具本身费用和刀具用量。刀具更换的频率主要与刀具寿命相关,刀具寿命的长短又取决于刀具的磨损程度。对于给定的材料、刀具和冷却条件,刀具的寿命主要由切削用量三要素——切削速度、进给和切削深度所决定。
2 刀具寿命、切削用量和机加成本之间的关系
像高温合金这样的难加工材料,机加工效率不会很高的最重要限制因素就是刀具的磨损。刀具磨损的主要驱动力是切削温度,由切削三要素(切削速度、进给和切削深度)、材料特性(硬度、导热性)、冷却液性能和冷却方式、刀具性能(种类、几何形状、涂层、厚度)、加工工况等几大因素共同决定。因此,刀具磨损的定量分析是很难的。不论是通过机械学或物理学为基础建立理论模型,还是基于实验数据建立经验模型,都很难建立起一个准确针对刀具磨损的函数模型。尽管已有一些学者建立了利用神经网络进行刀具寿命预测的数学模型,但因为是在特定的条件和刀具实验中测到的数据,且收集的数据量相对来说比较少,因此模型的准确性和通用性都有欠缺。目前还没有一个预测刀具寿命的函数模型,能够适用于所有的磨损情况。这其中非常重要的一个原因就在于,用于修正函数系数的刀具磨损实验是极其昂贵和费时的,尽管也积累了许多实验数据,但由于刀具和刀具间性能表现的差异性,也使得刀具磨损呈现随机性,结果必然就有一定的差异性。现阶段,很少有书籍或数据库中会包含关于刀具寿命的预估数据,即便像Sandvik和Kennametal这样的刀具巨头,也很少提供以推荐切削参数加工时的预测的刀具寿命,这一切都恰恰说明了刀具寿命难以准确的定量计算。
刀具寿命关于切削用量的关系可以用图1来表示。随着切削用量的增加,刀具寿命均呈下降趋势,且切削速度对刀具寿命的影响很大,进给和切深的影响相对较小。刀具的寿命直接由刀具的磨损量体现,如图2所示,是刀具磨损量随时间的变化趋势。想要刀具发挥到最大效用,便要将刀具尽可能用到寿命极限。
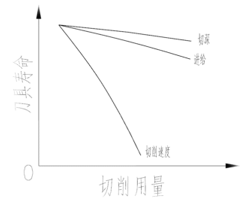
图1 刀具寿命曲线
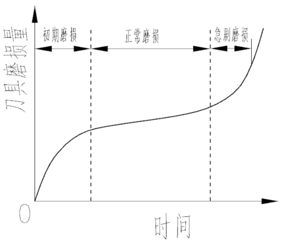
图2 磨损过程曲线
假设现在需要加工一个特征,如果所用刀具的寿命比需要的实际切削时间长,说明这把刀(刀尖)还可以继续加工一段时间,这时,总成本主要由机床成本决定。相反,如果所用刀具的寿命比需要的实际切削时间短,则加工完这个特征需要两个甚至更多的刀(刀尖),这时,总成本则主要由刀具成本(包括换刀带来的等待成本)决定。如图3,是成本关于切削用量的关系图。由图可可以看出,机床成本和刀具成本之间存在一个平衡,使得总成本最小化,寻找这个平衡点处的切削用量就是成本优化的关键。
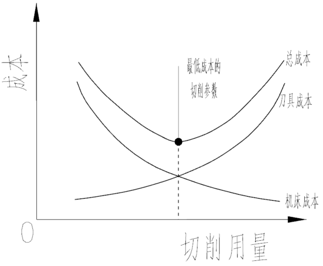
图3 成本曲线
3 机加工成本
加工一个工件的一道工序,一般会用到多把刀具,总机加工成本是每一把刀具加工时所对应的机床成本和刀具成本(刀柄费用多为一次性投入,这里不算在内)总和,故可针对每一把刀具来单独计算其对应成本,工序总成本即是多把刀对应成本的累加。
对于任意一把刀具而言,其对应成本可以用下列公式计算:
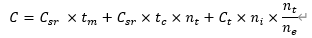
其中:
C:该刀具对应的总的机加工成本,单位:元;
C_sr:机加车间某类机床的成本费率,单位:元/分钟;
C_t:单把(片)刀具的成本,单位:元;
t_m:纯切削时间,单位:分钟;
t_c:单次换刀时间,单位:分钟;
n_t:换刀(尖)次数;
n_i:单把刀所含的刀具(片)数量;
n_e:单把(片)刀具的可转位次数;
举例说明:比如一把车刀用的是常规的432硬质合金刀片,成本是40元,该刀片可用刀尖为4个,即可转位4次;该刀片用来加工一个30分钟的特征,中途需要换一次刀尖;车间的所用车床成本是180元/小时,即3元/分钟,单次换刀时间是1.5分钟。基于以上数据,可知对于该把刀具所加工特征的机加总成本是:
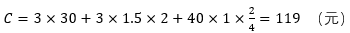
4 机加工成本优化
另外,加工时产生的残余应力,会造成工件变形,特别是航空零件,薄壁件偏多,且具有结构复杂、要求严格、工艺复杂、加工难度大以及工件易变形等显著特点,再加上航空零件的种类多、批量小、成本高的行业特点,使得航空零件在新品工艺开发时对于切削参数的选择通常会保守一点,以免加工过程中出现超差甚至报废的情况。参数的选择往往是基于以往经验,再结合每个零件的特点最终确定的。切削参数一旦确定后,一般情况下不会去改动,防止造成质量的不稳定。但是,节省成本是大势所趋,不得不对参数进行一定的优化。且随后的参数变更需要建立在反反复复的切削试验上。所以,在选择后续优化试验的切削参数时,有一个以机加总成本作为衡量标准的优化方法很有必要。
参数优化时,一般情况下不会去改动切深,主要原因如下:第一,切深是根据刀具性能和加工余量的多少共同决定的,再加上切深对刀具寿命的影响本身就比较小,所以新品开发时,切深的选择基本上已是比较合理的了;第二,改变切深就意味着重新编程,重新开发试切,时间长、任务重,风险大且收益很可能不高。因此,参数优化时,基本上都是从切削速度和进给入手,优化时只需要将速度和进给进行调整,刀具的切削轨迹不作任何更改,既方便又快捷,短时间内就会有试验结果。
尽管目前已经有相关学者针对刀具寿命提出了一些预测模型,尤其是基于神经网络的预测模型,预测结果的相对误差已经是比较小的了,但这种预测模型的样本数量太少,影响因素又太多,很难直接用到实际加工中。本文的重点在于成本优化,所以在刀具寿命层面的数据还是来自于传统的试验法,虽然效率低一些,但数据的准确性很好,实际参考意义较大。
以下是一把车刀在卧车(Okuma LU45)上加工Inconel 718的一组粗加工试验数据,切深恒定在0.8mm情况下进行的,试验了6种切削线速度,包括:30m/min、33m/min、36m/min、39m/min、42m/min、45m/min,分别在进给0.15mm/min、0.20mm/min、0.25mm/min、0.30mm/min时进行测试,收集刀具寿命数据,结果如表1所示。所用刀片是CNMG432刀片,刀具供应商是Sandvik,涂层S05F,机床冷却压力约为30BAR。
(注:刀具寿命的临界点很难界定和追踪,此试验测出的刀具寿命只是一个近似寿命。)
切削线速度
(m/min) 进给
(mm/r) 刀具寿命
(min) 切削线速度
(m/min) 进给
(mm/r) 刀具寿命
(min)
30 0.15 22 33 0.15 21
30 0.20 22 33 0.20 20
30 0.25 21 33 0.25 19
30 0.30 20 33 0.30 18
36 0.15 20 39 0.15 18
36 0.20 19 39 0.20 17
36 0.25 18 39 0.25 15
36 0.30 16 39 0.30 13
42 0.15 15 45 0.15 12
42 0.20 14 45 0.20 11
42 0.25 13 45 0.25 10
42 0.30 12 45 0.30 9
表1不同参数下的刀具寿命
成本优化就要建立在刀具寿命数据的基础上,下面举一个较为典型的实例进行说明。现有一个零件的某道车工序的外径部分需要用432车刀进行加工,工件材料、机床类型、刀片种类,冷却条件等均与上述实验数据一致。目前,工厂实际的参数选用的是:粗加工切削线速度33m/min,切深0.8mm,进给0.20mm/r。目前切削的相关信息包括:粗加工时间50.7min,刀片用量为3个刀尖,每个刀尖的加工时间基本一样(16min-18min),刀片使用程度估计在刀具寿命的70%-80%。
按照试验数据共计24组参数所使用的切削速度和进给,可计算出不同参数下的切削时间。换刀次数的最终确定,是在刀具切削时间达到刀具寿命90%左右的情况下所需的换刀次数(因为刀具存在不确定性,所以不能用到刀具寿命的极限)。有了切削时间和换刀次数,结合成本计算公式,可得不同切削参数下对应的机加总成本,如表2所示。(注:计算成本时的相关数据有:432刀片成本40元/片;车间的所用车床成本是3元/分钟;单次换刀时间是1.5分钟)
从表中数据可以看出,有两组参数可使总成本控制到90元以内,相比最初的成本133.4
切削线
速度
(m/min) 进
给
(mm/r) 切削
时间
(min) 换刀次数 总
成本
(元) 切削线
速度
(m/min) 进
给
(mm/r) 切削
时间
(min) 换刀次数 总
成本
(元)
30 0.15 50.7 3 195.6 33 0.15 46.2 3 182.1
30 0.20 38.2 2 143.6 33 0.20 34.8 2 133.4
30 0.25 30.8 2 121.4 33 0.25 28.0 2 113
30 0.30 25.8 2 106.4 33 0.30 23.5 2 99.5
36 0.15 42.4 3 170.7 39 0.15 39.2 3 161.1
36 0.20 32.0 2 125 39 0.20 29.6 2 117.8
36 0.25 25.8 2 106.4 39 0.25 23.9 2 100.7
36 0.30 21.6 2 93.8 39 0.30 20.0 2 89
42 0.15 36.5 3 153 45 0.15 34.1 4 160.3
42 0.20 27.6 3 126.3 45 0.20 25.8 3 120.9
42 0.25 22.2 2 95.6 45 0.25 20.8 3 105.9
42 0.30 18.7 2 85.1 45 0.30 17.5 3 96
表2不同参数下的机加总成本
元,节省了40元左右。根据测试实验以及加工后零件的平面度、圆度情况来看,两组参数均可以满足工艺要求,但39m/min的切削线速度和0.30mm/r的进给条件下加工出来的零件自由状态更好,因此最终选取此组参数作为成本优化后的参数。从优化后的结果可以看出,该工序外径粗加工参数的选择有些保守,没有完全发挥432刀片的切削能力,导致成本较高。对于参数优化还有几点需要补充说明一下:1)试验中切削线速度和进给的划分梯度太大,优化结果只是一个较优解而非最优解;2)以上数据均是试验情况下获得,与实际的批量生产之间有一定差距,参数优化时必须留有余地;3)成本优化必须建立在零件良好质量的前提下,尤其是对于精加工工序。
5 展望
对于工厂而言,在条件允许的前提下,如果能通过收集现有的加工参数数据,再辅以一定的切削试验,来测试出常用刀具的切削寿命,建立起一套较为完整的数据库,那么这将为成本节省提供更多的数据支持,也为以后新品开发阶段的参数选择提供依据,从而在源头上就可以适当引入成本优化,最终实现工厂效益最大化。
完全通过切削试验来得到刀具寿命当然是不理想的,如果能在综合应用文献著作、专家意见、试验数据、有据预测以及制造商推荐等资源的基础建立一个大概率的刀具寿命模型,就可以使刀具寿命的不确定性具体化,最终得到一个自适应的机加工成本优化模型:在最大期望成本节省的基础上,同时考虑刀具寿命的不确定性以及机加工时和刀具寿命间的平衡因素,来计算最优切削参数的迭代优化法。
参考文献
[1] 谭川,殷宝亮. 机加工工艺成本控制与优化途径探讨[J]. 内燃机与配件,2020,3(16):45-46.
[2] 陈伯仲. 提高机加工效率的方法分析[J]. 制造·材料:机械制造,2020,58(5):56-60.
[3] 徐营利,王展,胡晓兵,等. 基于径向基神经网络的刀具寿命预测模型研究[J]. 机械,2019,46(2):13-16,29.
[4] 侍红岩,吴晓强,张春友. 基于支持向量回归机的刀具寿命预测[J]. 工具技术,2015,49:47-50.
[5] 阳光,孟弘懿. 浅谈机加工工艺成本控制和优化途径[J]. 企业技术开发,2015,34(18):120-122.
