浅析高考复习中导数问题的几点策略
摘要:导数是高中数学学习的重难点内容,在高考试题中占据的比例较多,在大小题型中均有所涉及。随着教育改革的实施,高中新课程改革速度越来越快,高考中导数的考核范围得到了扩展,对学生的数学学习能力提出了较高要求。本文主要对近几年的高考考试卷进行分析,并介绍了高考复习导数问题的方法,希望可以给相关学者提供借鉴。
关键词:高考复习;导数问题;策略分析
导数在人们的日常生活中应用的较广泛,可以帮助人们快速的解决实际生活中遇到的问题,所以在高考中占据较大比例,进行考核时,主要从导数判断及单调性论证、函数极值及锥子等方面进行考核。因此进行高考复习时,也要加强研究,结合导数考题类型,针对性的提出复习方法,帮助学生简化运算,快速、准确的解决实际问题。
一、了解导数与原函数的关系
此类题型通常会给出学生导函数图像,然后要求学生根据导函数图像推导出原函数图像。解决此种问题时,学生应该首先对导函数正负区间进行分析,然后再了解导函数的增减区间,之后结合图像做出正确选择。此种题型考核时,主要用导函数正负表示函数单调性为正减负减变化,导函数零点决定了原函数的极值;此种题型虽然考核方法简单,主要从导数与函数性质进行分析,进行复习时,必须加强原函数与导数性质学习,了解两者之间的联系,然后实现知识的灵活应用。
二、利用导数几何意义,求解曲线切线问题
该题为某年高考原题,主要对函数求导及导数几何意义进行考核,该种题型几乎每年必出。已知函数 图像在点M(-1,f(-1))处的切线方程为x+2y+5=0,求解出函数y=f(x)的解析式。
导数几何意义是导数学习中的重难点,也是考核学生对理论知识灵活应用的主要方式,在高考中占据的比例也比较大,所以解题时,首先分析题意,然后借助导数意见,“导数在集合上表示切线斜率”进行运算。
从上述分析可知,第一,该题目主要考核导数的几何意义、切线方程及方程等相关内容,此种考核方式是导数的基本应用。第二, 的结合意义就是 在点 位置的切线斜率,可以将其切线方程表示为 。进行高考数学复习时,教师要重点给学生讲解此类题型的求解技巧,给学生布置较多的求解运算,让学生掌握多种题型的考核方式,鼓励学生大胆创新,同学间互相出题,让学生熟练掌握导数意义,帮助学生熟练的掌握该类题的计算方法。
三、求解极值问题
例题,已知函数 , ,a表示常数,求解当a=2时,函数 的极值。
经过对题目的分析可知,首先求解时,先确定出函数单调性,然后再求解其极值。
实际解题中可以借助函数图像进行分析,了解函数单调性变化,进而求解出函数极值。
从上述分析可知,利用导数方式求解极值问题时,如果函数f(x)在x0位置连续,此时可以采用下面的方法判断f(x0)为极大或极小值。第一,如果 ,而且在x0附近左侧 ﹥0,右侧 ﹤0,那么 就是极大值;第二如果在x0附近的左侧位置, ﹤0右侧 ﹥0,此时 就是极小值。
此类问题主要考察的是求导与求根的基础知识,主要利用数学分类思想进行计算。进行实际分析时,首先要确定出函数定义域,然后进行求导与求根计算,进而确定出函数单挑去见及极值。在复习过程中,教师要重点向学生灌输数学分类讨论思想,由于很多学生做题中并布置知道如何应用分类,有的学生没有经过探讨就得出答案,此种解题方法容易产生错误,所以教师必须加强分类思想教学,引导学生仔细分析题干要求,得出正确的答案。
四、实际应用问题
数学知识都是为实际所应用的,所以在数学考核中涉及的实际问题较多,主要对学生的综合应用能力进行考核,在高考复习中应该提高警惕。
例题,请学生设计一个包装盒,如下图1所示,ABCD是边长为60厘米的正方形硬纸片,去除阴影部分的四个全等的等腰直角三角形后,顺着虚线折叠,使得四个点与图中P重合,构成了正四棱柱样式的包装盒,E点与F点是AB上切掉等腰直角三角形后的两个断电,设AE=FB=x cm,如果广告商要求盒子容积V(cm)较大,此时应该取何值,并求出包装盒高与地面边长比值。
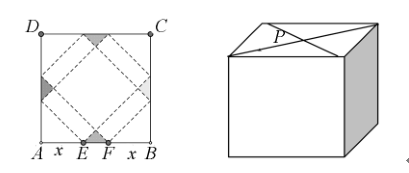
图1
此种问题求解是高考中常见的一种题型,进行解题时,首先要认真分析题意,然后构建数学模型,如果题型较复杂,还要应用导数求解函数最值问题,尤其要注意变量范围的变化。
五、参数取值问题分析
例题,设函数 ,其中a为实数,如果函数在 区间为单调减函数,对a取值范围进行计算。
计算该类题时,由于函数在区间上为单调递减函数,所以可以确定出函数在该区间的符合,然后将其转化为不等式成立,再利用函数问题求解最值问题。高数知识与不等式结合求解函数取值范围,是知识点汇聚的问题,主要考核学生对数学知识点渗透及综合应用能力,应该从思想上引起重视,做好此类问题复习。
结束语
本文主要分析了高考复习中导数问题求解方法,在导数复习中,今后还要加强数学思想的影响,主要利用数学结合思想、特殊化思想、分类讨论思想及转化思想,此种求解方式不仅能够增强学生的基础知识,还能够实现数学思想的结合。因此今后进行数学复习时,教师必须结合例题进行讲解,给学生灌输数学思想,帮助学生在做题中形成一套符合自己的学习方法,并将其灵活应用到数学导数求解张,得到较好的导数复习效果,提高学生的高考成绩。
参考文献:
[1]郑一平;苏华春.在比较中发现区别,在复习中改进对策——谈使用全国卷《函数与导数》的高考复习[J].中学数学,2016,(01).
[2]苏立标.高考导数复习中必须澄清的几个问题[J].中学数学月刊,2015,(10).
[3]杨大伟.以题代点谈导数应用的高考复习[J].理科考试研究,2015,(05)
[4]何拓程.纵览高考试题,漫话导数复习[J].中学数学教学参考,2016,(03).
