《勾股定理》课堂实录
教材说明:
华东师大版、八年级上、第14章、第1节。
任务单使用说明:
任务单提前一周下发,然后收上来,看看学生们做的情况,个别做的不是很认真的学生,也就是没有认真查找勾股定理的证明办法和相关故事的学生会要求其重写,教师也通过收、看任务单的过程逐步培养学生们的自学能力、掌握学生们的自学情况,适当调整教学过程中的细节。
任务单设计及教学想法:
勾股定理的证明办法大约有三、四百种,其中可以被初中学生理解且其思维方法很有代表性的至少有六、七种,而一堂课的容量有限,课时也有限,要想在有限的时间里让学生接触到这些宝贵的、具有极高价值的证明方法的话,就需要把任务提前下发,让学生通过自己的学习先接触、自行研究有关勾股定理的知识。任务单就是提供给学生一个自行研究学习的方向,学生可以通过他们熟悉的方式(比如在“百度”中)去需找答案。在课堂上,教师进行适当的穿针引线,把零散的知识串起来。
教学目标:会证明勾股定理,了解有关勾股定理的相关故事。培养学生发现问题、提出问题、解决问题的能力,
熏陶学生们的爱国主义情结。
教学重点:证明勾股定理。
教学难点:发现多种证明方法之间的关联,培养学生的分类、归纳、总结的能力。
课堂实录:
(课前屏幕上已经出示了课题)
师:关于勾股定理的任务单,我们已经在一周前就下发了,现在,我最好奇一件事:在我下发任务单之前,你们当中有多少人已经知道或是听说过勾股定理的呢?请举手。
(大多数孩子都举手了)
师:厉害!比我像你们这么大时有见识多了!现在就请同学们结合任务单中的第一题,看看谁能告诉大家:勾股定理的文字语言是如何描述的?
(学生回答)
师:非常准确!请坐,有谁知道它为什么叫勾股定理吗?
(学生回答)
师:太棒了!任务单完成得非常好!那它的符号语言又该怎么描述呢?
(学生回答:a2+b2=c2)
师:同意吗?
(学生间开始有争议,几个学生回答,互相补充)
师:所以,符号语言和文字语言要互相对应。由于,这是直角三角形独特具备的,因此,要先说明:“在Rt△ABC中”,同时,为了说明哪条边是直角边、斜边,我们还要点明哪个角是直角,才会有两条直角边的平方和等于斜边的平方。这就是它的符号语言。
(PPT展示)
师:换个图,他的符号语言又怎么说呢?(直角的顶点是A)
(学生回答:∵在Rt△ABC中 ∠BAC=90o∴c2+b2=a2)
师:非常好!请坐。现在,我们再来仔细观察这个定理,它实际上是在揭示一种什么关系?
(学生回答:三边关系)
师:三边关系?这么耳熟呢?我们在哪学过?(学生回答:三角形的三边关系:三角形的任意两边之和大于第 三边)直角三角形具备吗?(学生回答:具备)
师:也就是说:直角三角形不仅具备这种不等的关系,还具备今天我们将要学习的这种相等的关系。可是,怎 么来证明这种相等的关系呢?我们任务单中的第三题就是让大家用尽量多的办法去证明勾股定理。我在之前检查作业的时候也高兴地看到大多数同学都用了多种办法来证明。所以,接下来的时间,就是请同学们到前面来展示你们的学习成果。谁来?如果需要画图的话,不用担心,老师准备了足够多的全等的直角三角形,同学们只要直接贴在黑板上就ok了!
生: (学生上黑板前,为全体同学讲了下面的方法)
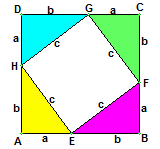
(以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于 . 把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上.简单证明如下:
∵ RtΔHAE ≌ RtΔEBF,
∴ ∠AHE = ∠BEF.
∵ ∠AEH + ∠AHE = 90º,
∴ ∠AEH + ∠BEF = 90º.
∴ ∠HEF = 180º―90º= 90º.
∴ 易证四边形EFGH是一个边长为c的正方形. 它的面积等于c2.
∵ RtΔGDH ≌ RtΔHAE,
∴ ∠HGD = ∠EHA.
∵ ∠HGD + ∠GHD = 90º,
∴ ∠EHA + ∠GHD = 90º.
又∵ ∠GHE = 90º,
∴ ∠DHA = 90º+ 90º= 180º.
∴ 四边形ABCD是一个边长为(a + b)的正方形,它的面积等于 2.
∴ . ∴ . )
师:太好了!还有别的办法吗?
生:(学生上黑板前,为全体同学讲了下面的方法)
(以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于 . 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.
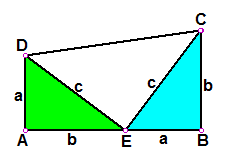
∵ RtΔEAD≌RtΔCBE,
∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90º,
∴ ∠AED + ∠BEC = 90º.
∴ ∠DEC = 180º―90º= 90º.
∴ ΔDEC是一个等腰直角三角形,它的面积等于 .
又∵ ∠DAE = 90º, ∠EBC = 90º,
∴ AD∥BC.
∴ ABCD是一个直角梯形,它的面积等于 .
∴ .
∴ .)
师:很好!这个可是一个有故事的证明呢,有谁知道?给大家讲讲!
(学生回答:用自己的语言讲了伽菲尔德的故事)
师:还有其他的证明办法吗?
生:(学生上黑板前,为全体同学讲了下面的方法)
(以a、b 为直角边(b﹥a), 以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于 . 把这四个直角三角形拼成如图所示形状.
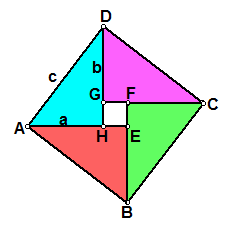
∵ RtΔDAH ≌ RtΔABE,
∴ ∠HDA = ∠EAB.
∵ ∠HAD + ∠HAD = 90º,
∴ ∠EAB + ∠HAD = 90º,
∴ 四边形ABCD是一个边长为c的正方形,它的面积等于c2.
∵ EF = FG =GH =HE = b―a ,
∠HEF = 90º.
∴ 四边形EFGH是一个边长为b―a的正方形,它的面积等于 .
∴ .
∴ .)
师:太好了!这个图的名气可不小,有知道他的来历的吗?
(学生回答:用自己的语言讲了赵爽的故事,讲了科学家大会的会标)
师:同学们可千万别小看了这个图,它足以说明赵爽是这个世界上“以形证数”的第一人!以后的科学家大多沿用并将其发展下去。还有别的证法吗?
生:(学生上黑板前,为全体同学讲了下面的方法)
(做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形.
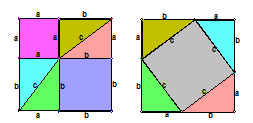
从图上可以看到,这两个正方形的边长都是(a + b),所以面积相等. 即 , 整理得 .)
师:这两个图联合使用,很巧妙。这个证明方法有出处吗?
(学生回答,说这是毕达哥拉斯的证明方法)
师:其实,关于他的出处是有争议的,有谁知道毕达哥拉斯发现勾股定理的故事,来给大家讲讲。
(学生回答:用自己的语言讲了毕达哥拉斯和地板的故事)
师:数学上我们把这种发现叫做:猜想。但,是否适用于所有的直角三角形呢?为此,人们投入了大量的实验验证过程。就是要画出许多不同的直角三角形,然后去度量三边长、计算、验证。今天,随着科技的发展,我们已经能够在几秒内解决古代人们上百年的验证过程。我们来看一下。(微机展示几何画板的动态过程)
但是,再多的实验数据也只是增添了实验的稳定性。特别的数据没有办法说明一般的规律,因此,数学家们又投入到了论证的过程。那么,争议就是:毕达哥拉斯自己论证出来了吗?现在,大约有两种说法:一种是他自己证出来了,就是上面的办法,一种说法是也许他证出来了,但失传了,有史料记载的最早的是希腊的数学家欧几里德给出了严格的证明。有没有同学知道这个欧几里德的证法的吗?能讲给大家吗?
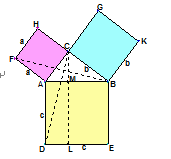
(学生上黑板来讲:做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使H、C、B三点在一条直线上,连结BF、CD. 过C作CL⊥DE,交AB于点M,交DE于点L.
∵ AF = AC,AB = AD,∠FAB = ∠GAD,
∴ ΔFAB ≌ ΔGAD,
∵ ΔFAB的面积等于 ,ΔGAD的面积等于矩形ADLM的面积的一半,
∴ 矩形ADLM的面积 = . 同理可证,矩形MLEB的面积 = .
∵ 正方形ADEB的面积 = 矩形ADLM的面积 + 矩形MLEB的面积
∴ ,即 .)
师:同学们听明白了吗?太棒了!你的任务单真是用心完成的!这个证明对于你们来讲还是有一定难度的。好了,同学们,我们已经找到了这么多证明的办法,咱们先停下来,回望一下,先别急着展示其它的证明办法,我们就先观察一下这几种办法,看看同学们有没有什么问题想要问的,或者是有什么发现想交流的?
生:第一种证明和第二种证明其实是有关联的,第二个图就是第一个图的一半。
师:非常好!这种证明有点像蚯蚓,我们都知道,蚯蚓一旦不小心弄断了身体很快就能再生,这种证明一样,截掉一部分,我们还能够证明原命题的成立,所以,我国著名的数学家张景中教授就把这种证明形象的叫做“再生的证明”。那么,在刚才同学们的证明基础之上,你能不能发现新的再生的证明呢?
(学生回答:第三种证明办法中,我们如果把G、E连上。应该可以继续证明这个命题的成立。我和孩子们一起探讨研讨,很有意思,鼓励孩子们继续发现新的“再生的证明”)
师:今天,尽管我们只是研究了勾股定理的若干种证明办法中的几种,同学们,知道勾股定理有几种证明办法吗?(学生回答)所以,今天我们研究的真的只是冰山一角,但是我依然感觉到了数学的千变万化带给我的震撼。我想,同学们一定也是这样的,所以,请同学们谈一谈:你此时此刻的感受和想法吧!
(学生回答)
师:谢谢你们的感受,我都体会到了,不过,我在你们刚刚说的过程中,突然有个问题想问:直角三角形中,两条直角边的平方和等于斜边的平方?那么,钝角三角形、锐角三角形是不是也有类似的结论呢?
生:大概会有:两条边的平方和大于或是等于第三条边的平方。
师:很好!这就是猜想,到底对不对呢?我建议,有兴趣的同学可以先进行验证:画出不同的钝角三角形、锐角三角形、然后去度量各边、在进行计算、看看是不是都成立,如果,都成立,你就可以进入到一个论证的过程,看看你能不能证明这个结论。我们都应该经历数学的这样一个过程:由猜想到验证到论证的过程,这是所有科学产生的过程。下一节课,就请同学们来讲讲你是怎样经历这样的一个过程的。好,下课。
