使用蚁群算法优化配置工具库的位置索引
文摘:生成切割工具最优位置索引对减少数控机器的非加工时间和优化计划过程是一个重要的任务。目前的研究工作提出数控机器执行某种特定制造业务,其切削工具库上应用了一个最优或接近最优位置索引的快速识别全球搜索技术--蚁群算法。目标函数是最小的索引时间。
关键字:索引时间、自动换刀、数控机床、优化、蚁群算法铣床。
1.介绍:
在今天的制造环境中,多个行业适应柔性制造系统(FMS)来应对不断变化的市场需求的竞争。FMS广泛应用于数控设备,由于在处理一个广泛操作的高灵活性,各种部件和兼容性在计算机控制系统下运作。当在最大程度上使用数控机器,整个系统的效率会增加。所以提高利用率,需要优化配置切削工具在工具库中的位置。
刀具在数控机床上的位置可以改变或自动被安装称切割工具子程序。刀塔用于数控车床和自动更换刀具的(ATC)铣床。本模型可用于ATC的刀库或数控机器上的刀塔。
索引时间被定义为在一个刀塔库或ATC走势之间的两个相邻的工具站或工具库持续的时间。双向索引工具库减少这台机器的非加工时间总是优先于单向的索引。在库的两个方向上旋转自动选择当前点和目标点之间的最近路径。目前的研究考虑双向运动的库。双向索引与单索引的区别为当前点和目标点的数量的计算,前者的值是小于或等于后者的一半。
Dereli提出目前的问题像“旅行商问题”(TSP),这需要完全的网络处理。他们应用遗传算法(GA)来解决这个问题。Dorigo[2、3]介绍了蚁群算法(ACA)解决完全的网络处理问题。ACA处理完全大型网络问题可以,比其他方法:遗传算法、模拟退火和进化编程,以最小的计算时间找到最优解。所以ACA一直扩充到解决当前问题。
2方法:
确定目前操作制造最优序列是一个先决问题。这序列通常是基于最小总决定设置成本。作者[4]提出的应用ACA找到一个最优的操作序列。一旦确定操作序列,以下方法可以用来实现最优的工具库安排。
步骤1最初一组刀具要求执行固定的制造业务被分配(最优)序列。每一个操作都是指派一个刀具。每个工具具有确定的数据属性。例:制造序列{M1-M4-M3-M2-M6-M8-M9-
M5-M7-M10}被分配了一套刀具{T8-T1-T6-T4-T3-T7-T8-T2-T6-T5}。刀具可以被解码为{8-1-6-4-3-7-8-2-6-5}。这里的序列制造M1需要刀具8,M4需要刀具1等等。总共有八个不同的工具,因此有八个可能序列在工具库中。
步骤2ACA是应用优化工具来找到最优的工具序列相对应最低的总索引时间。对于每一个序列算法所生成的相同序列的位置索引被分配(数字)。例如,生成序列的工具{4-6-7-8-2-5-3-1}按顺序分配到位置索引{1-2-3-4-5-6-7-8},即工具4是分配到第一的位置,工具6到第二位置等等。
步骤3计算不同后续切削工具数字然后总计确定每个旋转刀具部件的序列总数。在计算部件的数量从当前工具旋转到目标工具采取绝对误差。以下部分详细描述一个例子。
前两个操作M1和M4在假定操作序列分别要求刀具8和1。该工具生成的序列算法是{4-6-7-8-2-5-3-1}。在这个序列工具8和1放置在第4和第8(ATC)刀塔的位置索引。因此当前工具8达到目标工具1所需单位旋转总数|4-8|=4。同样的整个序列单位旋转所需的总数量是|4-8|+|8-2|+|2-1|+|1-7|+|7-3|+|3-4|+|4-5|+|5-2|+|2-6|=30。
步骤4最小总索引时间是目标函数。目标函数的值是总数乘旋转单位刀塔的赋值(ATC)索引时间。如果单位索引时间假定是4s,总所需的工具序列索引时间就为120s。
步骤5是迭代次数增加ACA收敛于最优解。
3.分配原则:
以下三种情况下为位置总数与刀具使用的总数。
案例1位置索引的数量等于切削工具的数量。
案例2位置索引的数量大于切削工具的数量:
(a)没有重复的工具。
(b)有复制工具。
案例3位置索引的数量小于切削工具的数量。
如果问题分为:案例1在工具库不多次设置重复切削工具总会增加机器的非加工时间。在案例2重复切削工具的影响应仔细测试,通常复制工具太昂贵。案例3使得发现刀具被第二次设置。然而,其他表现可能在案例2(b)和案例3。被复制的工具可以用于这样一种方式,在ATC没有向左卸载索引或向左卸载一些位置索引。
4.蚁群算法:
蚁群算法(ACA)是一个全集性的的优化方法,已成功地应用到解决不同的组合问题像旅行推销员问题[2、3]二次分配问题(5、6)和车间作业调度问题[7]。该算法是得益于现实生活蚁群的觅食行为中个体蚂蚁从一点到另一点沉积物质信息素的方式。更高的信息素路径会更可能被其他蚂蚁选择导致进一步放大当前的信息素。因为这种性质,一段时间后,蚂蚁会选择最短路径。适用于目前该问题的算法是下一节要描述的。
这里假设有数量“k”的蚂蚁和每个蚂蚁都对应于一个特定的节点。蚂蚁的数量等于节点的数量作用于调节制造操作。每个蚂蚁的任务是生成一个可行解,通过随意添加一个新的刀具到当前直到完成所有操作。一只蚂蚁坐落在位置“k”移动到位置“r”使用以下状态转换规则:
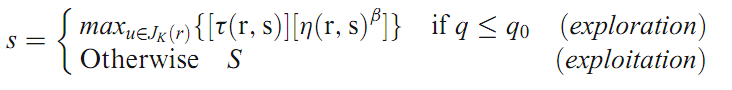
公式1
τ(r,s)被称为信息素水平,τ(r,s)随时间改变表明位置“r”移动“s”是多么重要。η(r,s)是一种启发式函数,它的效用评估移动“s”在“r”,而目前的工作,是逆数量单位旋转需要从“r”到“s”,参数“β”衡量启发式函数的相对重要性,“q”是一个价值选择的随机均匀概率介于[0,1],“q0”是一个参数。越小的“q0’就概率越高的做一个随机选择。总之“q0”确定探究公式1的相对重要性。
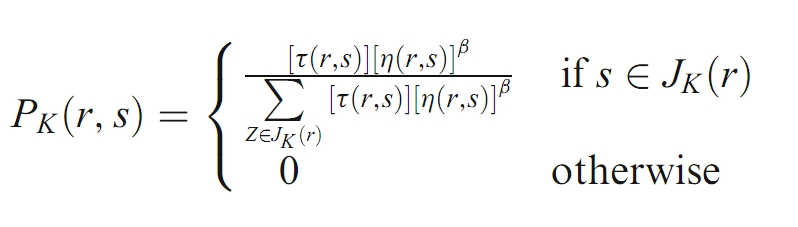
继续
公式2
Jk(r)代表位置的数量,指蚂蚁“k”到访位置“r”,S是一个随机选择变量根据分布给出了公式2,给出了蚂蚁从“r”选择去“S”的概率。
这个状态转换规则将有利于转换连接短边与高数量小道的节点。
4.1局部更新规则
建立一个解决方案,蚂蚁改变他们的轨迹通过应用以下本地更新规则:
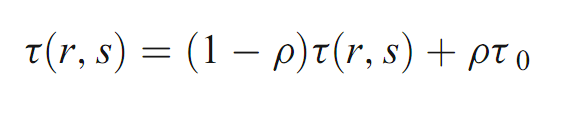
公式3
这里τ0代表初始信息素值。
4.2全球更新规则
一个更高更新的全球数量跟踪提供了简洁方案。从某种意义上说这是类似于一个强化学习计划,更好的解决方案得到更高的强调。
当所有蚂蚁都完成了他们的解决方案,边缘(r,s)属于最短的解决方案由一只蚂蚁的轨迹而改变,应用以下全球更新规则。
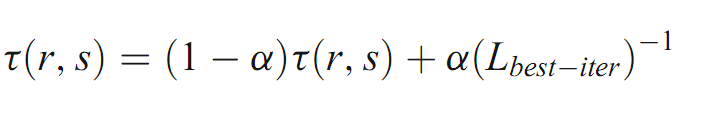
公式4
Lbest-iter是最好的解决方案在一个迭代中获得最小的总索引时间,“α”是信息素衰减参数,这是一个值在0和1之间,参数值[3]设置为β=2,q0=0.9,ρ=α=0.1。
4.3本地搜索机制
许多蚂蚁系统混合算法采用某种局部优化技术,如2选择技术、禁忌搜索、模拟退火等等。一旦每个蚂蚁已经建造了一个解决方案,这个局部搜索机制被用来进一步提高解决局部最优化和更新最后信息素水平的解决方案。这种集成显著提高蚁群算法的有效性和效率。目前,2选择技术用于本地搜索机制。
5.个案研究:
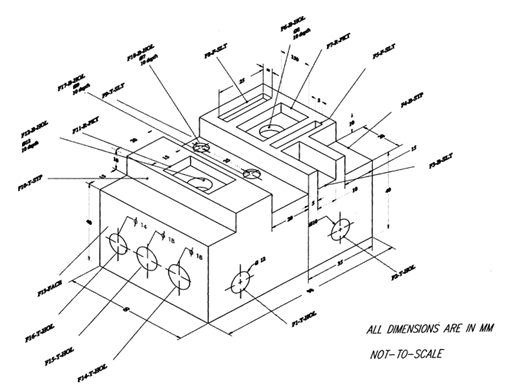
示例部分目前采取的操作如图1所示。它包含18个特征。特性和他们的缩写都列在表2。执行操作所需的特性都展示在表3。这个假定的操作序列和转位切割工具,每个操作见表4。最大数量的切割工具和ATC的索引时间分别为28S和0.69S。
示例 1
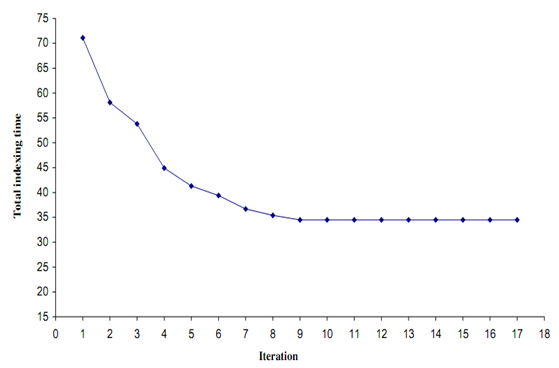
图表 1 收敛的ACA
图表 2 最优的刀具分配序列
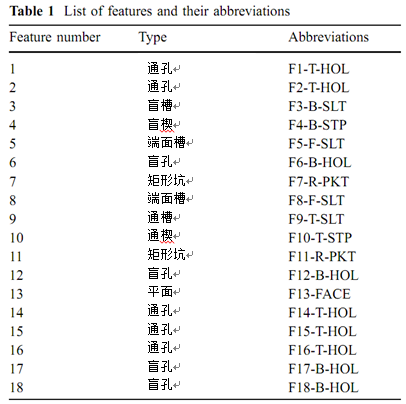
图表 3 功能及缩写列表

图表 4 特征及对应的操作

在工具库发现刀具位置的操作序列:M1-M2-M3-M4-M5-M6-M7-M8-M9-M10-M11-M12
-M13-M14-M15-M16-M17-M18-M19-M20-M21-M22-M23-M24-M25-M26-M27。相应的工具需要执行上面的操作顺序是T1-T1-T2-T3-T4-T2-T2-T2-T2-T5-T6-T5-T7-T5-T5-T8-T9-T5
-T10-T5-T11-T5-T12-T5-T13-T5-T14。
总数量不同的工具这里需要有14个,因此有14!种排序方式。
这里描述的问题为案例2(a) 位置的总数量大于没有重复的切削工具的数量。ACA是用来获取切割工具的位置,使得完成上述规定的固定操作序列总索引时间最少。
6.结果和比较:
最优序列的工具位置在应用ATC算法是T1-T2-T3-T4-T14-T6-T7-T10-T5
-T11-T12-T13-T8-T9。如示例2所示。
示例 2 ATC上最优的工具位置序列
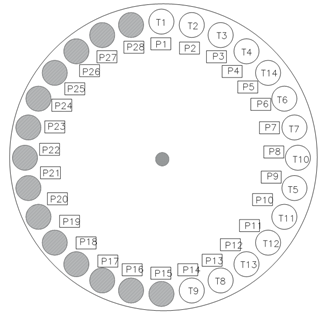
最优序列已经有50个部件旋转的ATC,换句话说总索引时间为34.5S。ATC越慢则增益越高。遗传算法(GA)的参数采取对文献[1]编码在Turbo c++和奔腾IV2.8 GHz处理器上执行。GA找到解决方法所花费的时间来是26 s。ACA执行时间为14S。显然,ACA比GA更快的得到了最优解。
图1展示了收敛的ACA。最好的解决方案是在每个迭代中获得逆的迭代次数。在第10次迭代得到问题的最优解。增加为18次迭代确保最优解。
7.结论:
由于目前的问题可以建模为一个旅行推销的问题,目前优化处理开发系统基于切割工具上使用ACA刀塔或数控机床的ATC刀库。甚至一个小的总索引时间将导致在大批量生产加工时间显著增加。这导致数控机床的利用率增加和整个系统效率的提升。
文献:
Dereli T,Filiz H(2000) 使用遗传算法分配最优位置索引工具集Robotics Auton Syst 33:155 – 167
Dorigo M, Maniezzo V, Colorni A (1996) 蚂蚁系统:由一群优化合作代理. IEEE Trans Syst Man Cybern 26(1):29–41
Dorigo M, Gambardella LM (1997) 蚁群系统:旅行商问题的合作学习法. IEEE Trans Evol Comput 1(1)53–66
Krishna AG, Rao KM (2004) 使用蚁群算法的优化操作序列CAPP. Int J Adv Manuf Technol (in press)
Gambardella LM, Taillard ED, Dorigo M (1999) QAP蚁群. J Oper Res Soc 50:167–176
Stutzle T, Dorigo M (1999) ACO算法的二次分配问题.在: Corne D, Dorigo M, Glover F (eds)新的优化思想 麦格劳-希尔,纽约
Colorni A, Dorigo M, Maniezzo V, Trubian M (1994) 蚂蚁系统与作业车间调度. Belg J Oper Res Stat Comput Sci 34(1):39–53
