非圆曲线数控车削编程
【摘要】数控车床编程加工只有直线插补和圆弧插补,不能直接进行非圆线曲线编程。为了进行非圆曲线编程,本文提出了以圆弧相切拟合和直线逼近拟合的方法编程,程序简洁,计算量少,加工精度高;而且只要作少量改变,就可以用于各种不同尺寸和形状的非圆曲线,重用率高,是一种高效率、高质量的数控车削编程方法。
【关键词】非圆曲线 数控车削 宏程序 拟合 计算
前言:
数控车床上,只要能编出程序,就可以车出需要的形状。对于一般的零件,其形状往往是通过直线与直线相交,直线与圆弧相交,直线与圆弧相切,圆弧与圆弧相交,圆弧与圆弧相切等各种直线与圆弧进行各种方式组合而得到。然而,还有很多形状,不管由直线与圆弧进行怎样方式的组合,都无法得到,如椭圆,如抛物线,如正弦曲线等三角函数曲线、螺旋线等。数控车床上,有直线插补、圆弧插补,可以直接编程序加工出由直线和圆弧组合得到的形状,却无椭圆插补、抛物线插补、正弦曲线等非圆曲线插补,也就无法直接编程序加工出这类形状。
那么,在数控车床上,加工非圆曲线时应如何编程呢?我们先看看数控车床是如何实现G01、G02和G03的。由数控车床的插补原理可知,数控车床的数控装置也并不是直线走出不平行于坐标轴的直线和圆弧曲线的,而是用直线段逼近的方法走出这类直线和圆弧的。也就是说,数控车床实际走出的不平行于坐标轴的直线并不和要求的直线重合,而是用一小段一小段的平行于坐标轴的线段或是与坐标轴成45度角的线段去近似走出要求的直线;数控车床实际走出的圆弧也并不和要求的圆弧重合,而是用一小段一小段的平行于坐标轴的线段或是与坐标轴成45度角的线段去近似走出要求的圆弧。只不过,数控车床在走直线和圆弧时,每走一步,都经过严格的计算,使误差达到了这台数控车床所能达到的最高精度,即误差不会大于这台数控车床的脉冲当量,数控车床的脉冲当量即决定了这台数控车床的最高精度,而一般数控车床的脉冲当量都远小于被加工零件的精度要求,所以加工出的零件的精度都能达到要求。
由此看来,我们也可以用数控车床上数控装置实现G01、G02和G03的方法拟合非圆曲线,编程让车刀走出非圆曲线。具体的方法有两种,如下:
一、 圆弧拟合非圆曲线
以椭圆为例,只要给出长短轴,就可以用四段圆弧近似画出要求的椭圆,哪么,就可以计算出这四段圆弧的半径和起点终点数据,编出椭圆加工程序,只不过,这样加工出的椭圆,误差是比较大,而且误差是固定的,不能根据实际零件的精度要求进行加工。
不过,如果能进一步,用更多的圆弧似合所要加工的椭圆,就能提高精度,并能按要求的精度加工,方法有两种:
一种为相邻两圆弧彼此相交,能保证按编程允许误差δ允计算节点坐标,计算过程相对简单,但由于圆弧相交,工件表面整体不光滑,零件表面质量不高。
另一种是相邻圆弧彼此相切,可保证在等误差的条件下,由一系列彼此相切的圆弧逼近曲线,工件表面整体光滑,零件表面质量高,但计算过程过于繁琐。
二、 直线拟合非圆曲线
用圆弧相切法拟合非圆曲线,节点少,表面光滑,程序短,表面质量高,但数学处理复杂,不同的非圆曲线要建立不同的数学模型,效率低。如果回头再看数控车床的插补原理,即可发现,从根本上说,圆弧插补最终实质上也是用直线拟合走出来的,只不过是节点间距小,从而精度高。所以,只要在精加工时取非常小的节点间距,甚至用脉冲当量作间距,就可以远远超过零件的加工精度要求,自然肯定能达到加工精度要求。在粗加工时取较大的节点间距,用G71或G72的走刀方式,需要的数据由宏程序计算,则完全可以达到G71G72的加工效率,这样,用直线拟合既能达到加工质量要求,也易实行。
因此,只要能建立准确的数学模型,就可以取得需要的数学公式,把数学公式编进宏程序,从而加工出达到规定精度要求的非圆曲线,下面举例说明:
(一) 椭圆
建立数学模型,如图1:
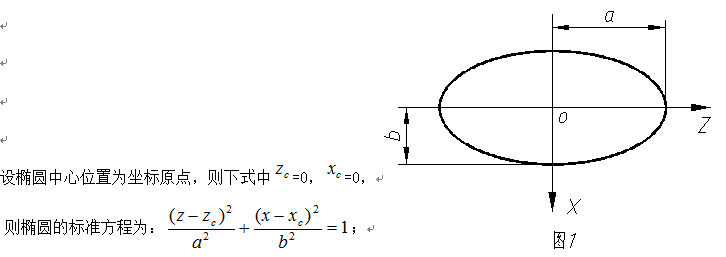
取X坐标为自变量,这样能准确确定每次粗加工的余量,Z坐标为因变量,则Z=a*SQRT[1-a*a/b*b];(用宏程序的方式表示)
应用举例:要加工下图所示零件:
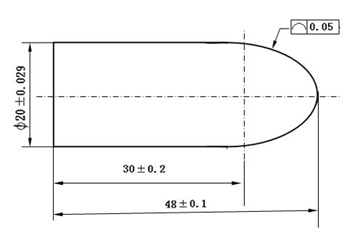
零件左边是直径为Ф ,长为 的轴,右边是长半轴 ,短轴半 ,焦点在 轴的椭圆旋转体,轴和椭圆旋转体相切。以椭圆中心为编程原点,即椭圆右端的坐标为(0,18),起始角为 度,终止角为 度,轮廓度公差为 。
设毛坯直径为Ф22 ,根据数据编出数控车床加工程序如下:
O0001;(主程序)
G00 X100 Z150; (刀架移到安全点)
M3 S2 T0101; (启动主轴,调用第一号刀外圆刀)
G00 X23 Z20; (外圆刀移到外圆循环起始点)
G90 X20.5 Z-35 F60;(粗车外圆,余量0.5mm)
#1=20;(X坐标变量赋初始值)
#2=0;(Z坐标变量赋初始值)
WHILE #2 GT 0 DO1;(粗加工循环)
#1=#1-2;(背吃刀量2MM)
#2=18*SQRT[1-#1*#1/100];(计算Z坐标)
G00 X[#1+2.5];(快速定位)
G90 X[#1+0.5] Z#2 F60;(粗加工至X[#1+0.5] Z#2)
END1; (粗加工循环结束)
M98 P0002 #3=0.2;(调精加工子程序半精加工,余量为0.2)
M98 P0002 #3=0;(调精加工子程序精加工,余量为0)
G00 X100 Z150; (刀架移到换刀点)
T0202;(换切断刀,刀宽3MM)
G00 X21 Z-33;(定位)
G94 X-1 F20;(切断)
G00 X100 Z150; (退刀)
T0100; (换回基准刀)
M30; (结束程序)
O0002;(精加工子程序)
G00 X0 Z19;(快速定位到精加工起点)
#4=0;(X坐标变量赋初始值)
#5=18;(Z坐标变量赋初始值)
WHILE #4 LE 20 DO1;(精加工循环)
G01 X[#4+#3] Z#5 F20;(精加工至X[#4+#3] Z#5)
#4=#4+0.01;(间距0.01MM)
#5=18*SQRT[1-#1*#1/100];(计算Z坐标)
END1; (精加工循环结束)
Z-35; (精加工到Z-35)
G00 X21;(快速回刀)
Z19;(快速回刀)
M99;(返回主程序)
可见,椭圆弧部分加工程序十分简洁,而轮廓精度达到要求,加工质量高。
(二) 抛物线
建立数学模型,如图2:
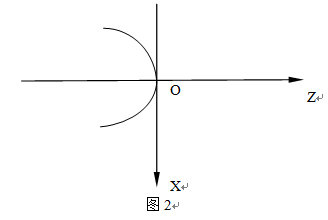
取X坐标为自变量,这样能准确确定每次粗加工的余量,Z坐标为因变量,则z=-x*x/10;(用宏程序的方式表示)
实例:要加工下图所示零件,右边为抛物线z=-x*x/10:
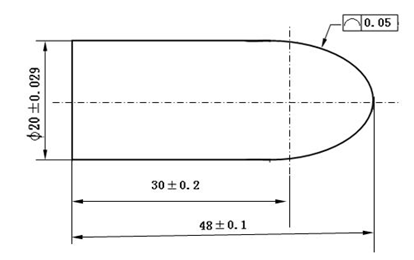
零件左边是直径为Ф ,长为 的轴,右边是方程为z=-x*x/10的抛物线旋转体。以零件右端中心为编程原点,轮廓度公差为 。
设毛坯直径为Ф22 ,根据数据编出数控车床加工程序如下:
O0001;(主程序)
G00 X100 Z150; (刀架移到安全点)
M3 S2 T0101; (启动主轴,调用第一号刀外圆刀)
G00 X23 Z20; (外圆刀移到外圆循环起始点)
G90 X20.5 Z-35 F60;(粗车外圆,余量0.5mm)
#1=20;(X坐标变量赋初始值)
#2=0;(Z坐标变量赋初始值)
WHILE #2 GT 0 DO1;(粗加工循环)
#1=#1-2;(背吃刀量2MM)
#2=-#1*#1/10;(计算Z坐标)
G00 X[#1+2.5];(快速定位)
G90 X[#1+0.5] Z#2 F60;(粗加工至X[#1+0.5] Z#2)
END1; (粗加工循环结束)
M98 P0002 #3=0.2;(调精加工子程序半精加工,余量为0.2)
M98 P0002 #3=0;(调精加工子程序精加工,余量为0)
G00 X100 Z150; (刀架移到换刀点)
T0202;(换切断刀,刀宽3MM)
G00 X21 Z-33;(定位)
G94 X-1 F20;(切断)
G00 X100 Z150; (退刀)
T0100; (换回基准刀)
M30; (结束程序)
O0002;(精加工子程序)
G00 X0 Z19;(快速定位到精加工起点)
#4=0;(X坐标变量赋初始值)
#5=18;(Z坐标变量赋初始值)
WHILE #4 LE 20 DO1;(精加工循环)
G01 X[#4+#3] Z#5 F20;(精加工至X[#4+#3] Z#5)
#4=#4+0.01;(间距0.01MM)
#5=-#1*#1/10;(计算Z坐标)
END1; (精加工循环结束)
Z-35; (精加工到Z-35)
G00 X21;(快速回刀)
Z19;(快速回刀)
M99;(返回主程序)
可见,抛物线部分加工程序十分简洁,而轮廓精度达到要求,加工质量高。
(三) 其它非圆曲线的处理
若编程加工其它非圆曲线,先建立适当的方程,根据方程建立相应的数学模型,用同样的方法试取拟合点,解出拟合点的坐标计算公式,编进宏程序即可。
总结:
圆弧拟合,表面上看加工表面光滑,实质上还是用直线插补走出的,却带来数学处理复杂,要另外编程计算节点,通用性低的问题。而直线拟合,只要取较小的间距,就能达到同样的加工表面质量要求,但数学处理简单,通用性强,而且可以用宏程序编程,免去另编程计节点及相关数据的麻烦,效率高,为加工各种方程曲线和扩展数控车床的功能提供了极大的方便。
参考文献:
[1]《数控编程》第二版,全国数控培训网络天津分中心组编,机械出版社,2006年。
[2]《数控宏程序编程方法、技巧与实例》冯志刚, 机械工业出版社,2011年5月。
[3]《数控加工工艺学》,中国劳动社会保障出版社,2000年。
