矿物表面接触角测量及其适用性技术概述
摘要:利用浮选法可以从矿物中分离有价值的部分,为了提高浮选效率,矿物表面的润湿特性研究起着至关重要的作用。由于接触角与矿物的可浮性有着密切的关系,因此它的值是一个有用的指标,故可以用其来表示固体矿物表面的疏水特性。
本文中,将对矿物表面接触角测量及其适用性技术进行综述。对于接触角的测量,主要有两种技术是可用的,其中一种适用于光滑和平坦的表面,而另外一组已发展为适用于非理想的表面或颗粒。在实际矿物接触角测量过程中,毛细管渗透法相比其他测量方法显得更适用。然而,实验过程中需要的制样技术,以及更重要的是对滞后接触角进行必要的修正,成为这种技术的主要挑战。接触角精确地测量与实际的(批处理)浮选数据的耦合,这还是一个需要继续研究的领域。
关键词:接触角 疏水性 泡沫浮选
1.介绍
在选矿过程中,矿物质经研磨后从矿石中解离出来,浮选依据矿物自然或人工疏水性的差异而被广泛用于从脉石矿物中快速、高效的分离出有用矿物。疏水性的矿物颗粒更容易粘附气泡并漂浮到矿浆表面,而亲水性的矸石则不会发生上述行为并留在尾矿中。
总体而言,浮选过程主要可分为三个子过程;颗粒与气泡碰撞,颗粒粘附到气泡表面,颗粒最终脱离气泡。为了使以上过程变得复杂,可以进一步通过向矿浆中加入多种试剂来控制颗粒的表面性质和矿浆化学性质。对于浮选来说,主要的必须条件是气泡取代矿物表面的水,并且这种取代作用可以用后退接触角来量化。很显然,掌握矿物表面化学性质和润湿性在控制泡沫和矿物粘附等子过程起着至关重要的作用(Wark,1984)。然而,为了改善浮选过程而进行的更进一步的研究工作,现在还从在一定的差距。我们正在开展不同的方法,包括建模,理论以及实验研究,并在这些基础上认真努力弥补这一差距。在澳大利亚联邦科学与工业研究中心(CSIRO),量化流体动力组织(CFD)目前正在开发研究机械搅拌式浮选机,在开发过程中,接触角的输入量一个重要的输入参数,它影响着该模型的准确性和适用性(KohandSchwarz, 2003, 2006)。这种模型的成功之处在于,在现有的设备和操作改进方面,它可以提供显著地成本节约,并达到改善浮选性能的效果。因此,重要的是实现对矿物样接触角准确地测量,以及精确量化各种因素的影响。
由于接触角和矿物可浮性之间的密切关系,所以接触角是一个有用的指标。多年来,已开发了许多不同的技术来测量接触角。然而,争议仍然笼罩在文献所提供数据的准确性和数质量上,以及其是否适合使用杨氏公式,这一点稍后将做讨论。而对于实际的矿物系统,只有少量可用的技术不受无理的要求和假设的约束,提供精确的,有意义的和现实的接触角值,
本文旨在审查可用的接触角测量技术,特别是那些适用于矿物表面,分析它们的优缺点 ,并确定可能的改进方法和使其适应实际矿物表面,以进一步了解它们在泡沫浮选过程中的实际应用情况。大多数主要的接触角测量技术及实验室设备已被描述Adamson and Gast (1997), Hunter(2001), Ralston and Newcombe (1992) and Kwok and Neumann(1999)。归纳一下,这些测量方法可以大致分为两类,其中一种是适用于平坦和光滑表面,而另外一种可用于非理想的表面或颗粒,也可说是更相关真实的矿物表面。这里将介绍最新提出,经严格审查的技术。
2.背景
对于三相接触线的固体表面/水/空气的接触角的研究有两个步骤。可以把一滴水放置在固体表面上,如示于图1(左);或者,也可以用浸没的气泡来探测浸渍于水中的固体,如示于图的表面1(右)。后一种方法是相关的,几乎是强制性的研究矿物浮选中,矿物颗粒在水介质中力度大小合适的相互摩擦碰撞的表面反应,在原则上,这两个接触角是相同的。
如图所示,1(右),在水性介质中,无机固体表面上的气泡接触角θ被定义为在三个界面张力的作用下,气泡的力学平衡:固-气(γs/a)固-液(γs/l)和液-气(γl/a)。这个平衡关系被称为杨氏方程式所示。
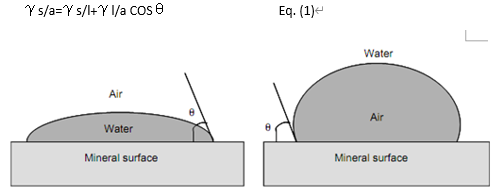
图1.固体表上,空气中的水滴形成的接触角(左),水中的气泡形成的接触角(右)
杨氏方程的有效性要求固体表面是光滑,平坦的,均匀的,惰性的,不溶性的,非反应性的,非多孔的,和非变形的质量。这些条件通常是不符合实际表面的(Kwok et al., 1998; Lam et al., 2002; Tavanaet al., 2004)。理想表面接触角的测量和实际矿物表面接触角的测量之间的差异,以及为了使它们适用于测量,在制备矿物表面时的建议及解决方案,如表1中。值得注意的是,对于所有实际的矿物样本,在一定程度上都存在粗糙表面和化学非均质。因此,接触角可能沿着接触线从一个点到另一个点发生变化,将分化为三个定义,如图2所示(Marmur,1996)。一个理想固体表面预期的“内在的接触角”如图,2(左)所示;一般的光学方法测量接触角,这种方法将在第3节详述,将产生“明显的接触角”。这个角是光滑固体表面的切线方向与气-水界面切线方向的夹角,如图2(右)所示。在完全平滑的固体表面上,表观接触角与实际的接触角是一致的。而在实际矿物表面上,这两个值可能有很大的不同。
理想的表面特征 实际矿物表面特征 建议的解决方案
光滑 粗糙 参考Wark and Cox (1934)的建议
平坦 不规则的形状 使用切割锯,但很难获得具有足够尺寸的矿物样品
均质 异质 使用合成样品,但这不是真正的矿物样品
惰性的、不溶性的、非反应性 变量 在适当的条件或解决方案下准备和储存样品
非多孔 变量 对于大多数金属矿是非必须的
非变性 非变性 对于大多数金属矿是非必须的
表一:理想表面与实际矿物表面接触角的测量的对比,以及在制备矿物表面时,使它们适用于测量而提出的一些建议与解决方案。
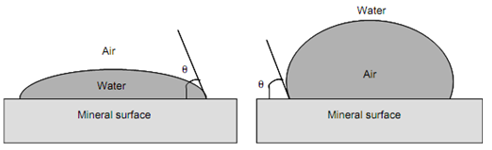
图2. 固有接触角(左)与表观接触角(右)之间的不同
实际表面的表观接触角不是唯一的,而是成或多或少的幅度在前进(最大)和后退接触角之间变化。而这两个值之间的差异被称为接触角滞后。Butt et al.(2006)提出这个滞后值通常在5o到20o之间,但有时也会显著性增高。Adamson and Gast (1997)提出了三个主要原因导致滞后;污染的液体或固体表面,表面粗糙度,表面上固定的具有一定规模的大分子。遗憾的是,没有独立的方法区分造成接触角滞后的原由。因此,在制造矿物表面时就会有一种独特的想法:尽可能接近完美,以得到最小或可忽略不计的接触角滞后。
在浮选过程中,如果一种矿物的接触角是0o,这就意味着水润湿矿物优先于空气和空气-矿物的接触,然而,这是不可能的。接触角为0o,代表没有可浮性;相反,接触角为180o,代表矿物通过空气完全润湿而排斥水。众所周知,没有一种矿物的气-水接触角大于110o,因此便无法实现180o接触角的实验条件。
3.接触角测量
一般情况下,接触角测量技术可分为两大类:在平坦表面测量和非理想表面或颗粒的测量。
3.1平坦表面
这里存在几种在水平和垂直平坦表面测量接触角的技术。接触角测量最常见的方法,涉及使用低倍率光学装置观察液滴或气泡图像。由于在一个露天的实验室环境中保持矿物表面不受污染是很困难的,因此得到一种干净、平坦的矿物表面是相当困难的,这种表面在实验中总因可得到重复结果而受到欢迎。由Wark and Cox (1934), i.e.提出的表面制备实验过程,即在严格控制的条件下在水中研磨或抛光,已被发现实验重现性好,并且可以得到特殊的平衡角度。平坦表面上接触角测量的成功很大程度上依赖于表面质量和其清洁度,得到的接触角值可能介于前进θa和后退接触角θr之间。一般情况下,当接触角小于20o时,由于其高的灵敏度实验误差,平坦表面接触角的测量是困难和不确定的(Gaudin, 1957)。
3.1.1液滴剖面
对于平坦固体表面接触角测量,最广泛使用的技术是通过查看液滴剖面直接测量角度,
毕格罗等(1946)表明一个显微测角仪可以用来查看一滴水置于抛光面并测量接触的剖面。一个停止压扁或附着气泡的图像可以被投射到屏幕并进行轮廓追踪,随后由量角器测量角度。另外,Leja and Poling (1960)提出一张图像也可以采取永久保存。要想提高精度,可以通过使用相对高的放大倍数(最多50),这样的精度就允许详细审查液滴剖面并进行固体表面的交集。Hunter (2001)提出由一个固着液滴或附着气泡形成的角,当这个角大约大于20o时,测量精度可以达到±2o。
Taggart (1930)等人介绍的补泡法是另一种形式的剖面法。由于它没有放置在剖光表面而不同于其他气泡,而在它上面,表面张力形成的的支持力被用来保持系统的稳定,正如浮选系统。Wark and Cox(1934)表明,气泡无论是自由悬浮,还是受玻璃容器的束缚,接触角都是相同的。
液滴剖面技术可通过分别增加和减少液滴的尺寸来测量前进和后退接触角。此外,所观察到的接触角有可能发生变化,具体则要取决于表面活性剂是否达到吸附平衡。
使用这种方法有两个优点:测量时仅仅需要非常少量的液体和小到几平方毫米可以利用的固体表面。然而,这种优势也是这种技术的缺点,它存在着较高的风险,以及受到杂质的影响。该技术的另一个限制是,相机或成像装置将集中在最大的子午线截面中,因此只反映该点子午面内相交的三相线上的接触角。表面异质性和粗糙度的变化很可能导致接触线沿着三相线变化。此外,接触角对液滴大小的依赖性将会导致系统出现问题。总而言之,在精度要求不是很高时,这种测量技术是最方便的。
3.1.2液滴维度
当液滴的尺寸取决于一个表面时,接触角可以通过液滴维度来进行测量。这种液滴可能不需要完美的轴对称性,但一个对称形状提供的优点在于,可以用润湿液体的表面张力同时确定接触角。这种方法包含一些测量参数,基于拉普拉斯方程(Eq. (2))描述液体表面的形状,这些参数可以确定液滴的轴向对称性。R1和R2代表两个主曲率半径,DP是内外界面的压力差。
ΔP=γ(1/R1+1/R2) Eq. (2)
Bashforth and Adams (1883)是第一个作出努力,即利用拉普拉斯方程,从理论化学的角度来描述液滴形状,Fisher (1979)为了测量固着液滴较小的接触角,努力研究了接触角与半径和体积之间的关系。即用一个分析天平来确定质量,用一个已知的密度来确定体积,以及从液滴的照片中确定液滴半径。基于拉普拉斯方程的数值积分和Bashforth and Adams (1883)图表,这种方法不断在深入研究,并已得到改善。
尽管该方法不断地改善,但在算法方面仍存在几个缺陷。通常我们根据测量点与计算曲线的水平距离计算平方和,并得到误差函数。然而,这种测量方法可能是不够的,特别是对于形状深受重力影响的固着液滴,此时为了获得一个准确的接触角值,达到最佳的拟合曲线起着关键作用。因此,这项技术已通过了修改,客服这些不足之处,并达到一个新的水平,称之为轴对称滴形剖面分析(ADSA)技术。
3.1.3轴对称滴形剖面分析(ADSA)技术
ADSA技术是一种根据固着液滴或悬挂液滴轴对称半月板的形状,来确定气-液界面表面张力和接触角。这项技术首先由Rotenberg (1983)等人提出,随后由Spelt(1987)等人和Cheng et (1990)进行推广和发展。该技术有两个主要假设:第一,实验液滴是拉普拉斯算子型并具有轴对称性;第二,重力是唯一的外力。ADSA-P提出了一种理论剖面,即从提取的实际液滴图像中,发现最匹配的液滴剖面,进而从其中可以计算表面张力,接触角,滴体积和表面积。其采用的方法基于拉普拉斯的毛细作用,通过把表面或界面张力作为一个可调参数,使实际液滴的形状与理论液滴形状相匹配。使其能够最佳识别正确的表面或界面张力,以及接触角。值得一提的是,这种方法与液滴剖面法不同:液滴剖面法提出用切线来确定液滴剖面,而ADSA技术是利用匹配的拉普拉斯算子形状来确定液滴的剖面。因此,在ADSA技术中需要一个完整的,不受干扰的液滴剖面,而如前面提到的液滴剖面技术,将一个针头深入到液滴中是不被推荐的。
Del Rio (1998)等人提出的ADSA-P技术更可靠,对于表面异质性和粗糙敏感度小,因此其更适合矿物表面。Rodriguez-Valverde 2002)等人提出捕收泡沫的方法搭配ADSA-P技术,就可以实现在多孔矿石中,方便、自动、可重复性的测量接触角。
3.1.4Wilhelmy方法
这种简单的方法,归功于Wilhelmy,故命名为Wilhelmy。当一个薄的,光滑的,垂直板,如显微镜载片或铂箔片,接触到一种液体,如果接触角小于90o,平板上将会施加一个向下的力WF(Eq. (3))
WF=PγLVCOSθ Eq. (3)
其中p为接触周边的长度。如果浸入的深度不等于零,则液体的体积V将被取代。因此,当考虑平板上施加的外力时,必须考虑其受浮力的影响。用以下方程描述Eq. (4)
WF= PγLVCOSθ—VΔρg Eq. (4)
因此,如果表面张力是已知的,则接触角是很容易计算的。通过向上或向下移动一个已知周长的光滑平板,就可以知道前进或后退接触角。虽然起初Wilhelmy法似乎是一种理想的方法,但它仍然存在几个缺点:第一,在操作过程中,其必须需要高灵敏度的电子秤。第二,测量过程中的步骤不必太多,在操作时,产生的蒸汽不应吸附到平板上。第三,这个平板必须具有恒定的周长,以及在平板上,所有表面具有相同的组成和形态。第四,对于锋利的边缘角落,需要尽量减少边缘或拐角效应,由于这些条件的难以完全满足,特别是对于真正的矿物标本。因此Wilhelmy方法也不被推荐。
3.1.5垂直板毛细液相上升
Wilhelmy技术可被修改,以便在垂直板上测量毛细液相的上升量h。当一个液体和一个垂直、无限宽的板相接触时,液体将会上升,它上升的高度可以通过拉普拉斯方程随时确定,得到Eq. (5)。
Sinθ=1-(Δρgh2)/(2γLV) Eq. (5)
知道液体和蒸汽之间的密度差Δρ,应重力而引起的加速度g,液体的表面张力γLV。则接触角θ就可以从测量的毛细管上升量h得到。出于实用的目的,板宽度2cm就可以满足无限宽的理论要求。因此,接触角的测量任务就被减少到只需测量一个长度,它可以用光学仪器完成,例如,测高仪。这种测量方法在Budziak and Neumann (1990) and Kwok (1995) 等人的在研究下已经了实现自动化,并用于执行各种动态的前进和后退接触角的测量。此方法已被证明特别适合用于测量对温度有依赖性的接触角。对于一个典型的液体来说,测量所得θ值的不确定性大约为0.1o。这种方法相对于Wilhelmy法的缺点是,该液体的表面张力γLV必须是已知的,如果溶液中含有表面活性剂,这将有可能是一个严重的不确定性。在这样的系统中,表面活性剂将被各种介质表面的吸附,有可能使表面张力和接触角同时发生变化。Wilhelmy法和毛细上升的联合使用,允许在同一时间通过求解方程(2)与(5)与目标三角函数COSθ2+SINθ2=1,来确定接触角和液体的表面张力。
3.1.6显微镜法
单一的胶体粒子在水溶液中接触角测量,这些年来,由于使用先进的显微镜方法,如原子力显微镜和共聚焦显微镜,已经发展与改进了很多。
根据Ducker. (1994), Preussand Butt (1999) and Ralston (1999)等人提出,利用原子显微镜(AFM),测量胶体粒子与水溶液中泡沫之间的相互作用力,可以确定单个粒子的接触角,然而,它仍建立在几个假设之上,以及其分析过程有点模棱两可,并且缺乏复杂的实验装置和必要的实验结果的校准。因此,它是一个不受欢迎的接触角确定方法。如Johnson 等人 (2006)的解释。此外,由于颗粒压实过程和气泡弹性形变引起的颗粒形状的改变,将会导致它们润湿性的改变。(Preuss and Butt,1999).Nguyen.(2003)等人提出,由于三相接触的位置相对于粒子是未知的,因此,很难确定测量的接触角是否可以作为一个标准,以及无法判断能否用其来衡量固体颗粒表面的疏水性。虽然结果表明AFM似乎是一个有用的工具,可以用来确定单个粒子的接触角,并提供有价值的分子间作用力,但是,在可变性表面,利用原子力显微镜测量是非常困难的,因此,这方面还需要进一步的研究。
共聚焦显微镜技术,这种用于单个直径为3—10um微玻璃纤维球接触角的测量技术,是被Mohammadi(2003)等人开发的。然而,这种方法较悬滴法相比,其结果似乎被高估,通过研究发现,荧光染料的不同和低精度悬滴技术是造成这两种方法差异的原因。
3.2非理想表面和颗粒
对于矿物应用来说,非理想表面和颗粒接触角测量是及其重要的,然而,因为其经常产生高度不可靠的结果,其又相当具有挑战。在非理想表面测量接触角,为了有一个完整的评述,将在第3.2.1节详细介绍这种测量方法的内容。对于粉状固体,由于粗糙度和孔隙度的影响,固体颗粒压缩成团得到的接触角比该固体光滑试样的要小。在Hunter (2001)评论的有关于接触角测量方法的文章中,对于压缩成团的固体来说,他是这样评价的“作为最好测量的试样,得到的接触角值却是无用的,如果应用不当,还会有误导作用”。在平板上测量的接触角其可靠性和适用性存在质疑,并且单一颗粒表面上的测量不能代表矿浆中的矿物颗粒,所以在实际矿物的情况下也是可疑的。此外,在平坦平面的制造过程中,清洁的、适合切割的、并且具有足够的尺寸,这样的矿物表面很少是可用的。由于实验条件难以达到,如上述显微镜法提及,因此胶体粒子接触角的测量是不常见的。通常用一个平均值来代替获得的许多颗粒的接触角的值。在填充床中,不规则颗粒润湿性的量化方法已被开发出来,并发现是更适用于浮选过程,它对于粒度范围为10um-200um、形状不规则矿物颗粒的浮选特性更为敏感。在填充床中,粉末状固体接触角的测量,称之为毛细管渗透方法,这种方法可以减少与单表面研究相关联的问题,毛细管渗透方法将在3.2.2中详细介绍。
3.2.1非理想表面的ADSD-D法
对于非理想表面(例如,粗糙的表面),接触角由于形态和能量的缺陷通常很难获得,这将导致三相接触线的凹凸不平,或在某些情况下,接触角值变小。由于缺乏一个清晰的三相接触点,在这些情况下,很难通过找到的液滴剖面来测量接触角。
对称液滴形状分析直径(ADSA-D),是ADSA的另一个分支,即从获得的液滴顶视图中,从上面查看液滴,可以获得准确和一致的接触角。在ADSA-D方法中,当接触周边,液体表面张力,和液滴的体积已知时,就可以通过毛细作用的拉普拉斯方程的数值积分来确定接触角Eq.(3)。这种方法适合用于测量较小的接触角(<20o),在不完善的固体表面上测量的接触角也可能是有用的,如木头和石块,尽管还需要进一步的改善。Rodriguez-Valverde(2002)等人提出,在接触角测量时,量化表面粗糙度效应是有困难并且存在争议。他们宣称,由于存在的亚稳状态和接触角对液滴尺寸的依赖性,平衡接触角是无法测量的。
3.2.2毛细管渗透粒子法
众多定性渗透技术被用于大多数处理压缩粉末的方法中:Washburn(1921)研究了动态技术, 随后这项技术由Levine (1980)等人推广发展,并由Fisher and Lark (1979)仔细研究了在狭窄的毛细管中的现象。后一种技术,基于毛细管压力驱动流体,并以一个可观察的速度通过粉末填充床的毛细管,主要用于确定粉末的接触角。静态测量最初由Bartell and Osterhof (1927), Bartell and Whitney (1932), and Bartell and Walton (1934).提出。随后由White (1982),对这种方法的理论基础进行延展研究。在一列填充粉末的毛细管中,润湿液体上升到一定的高度,这一列液体引力与毛细管压力平衡。另外,对于刚刚停止的毛细现象,外部压力差可以被加到与毛细管压力相反的测量压力差ΔP。
液体在拉普拉斯压力的驱动下,进入毛细管,可以通过以下的拉普拉斯方程(Eq.(6))进行描述。
ΔP=(2γLVCOSθp)/reff Eq.(6)
White (1982)定义了有效地毛细管半径reff如以下公式(Eq.(7))
reff=2(1-φ)/φρA Eq.(7)
其中,Φ是填充床中固体的体积分数,ρ是该固体材料的密度,A是固体的比表面积。结合(Eq.(6))和(Eq.(7))获得Laplace–White方程Eq. (8),在多孔介质中,对于Δρ来说,这是一个严格的热力学表达式。
ΔP=γLVCOSθφAρ/(1-φ)
Dunstan and White (1986)用毛细管的方法,利用清洗和化学处理的光滑玻璃小球。对White的方法进行测试,并获得了理论和实验之间密切联系关系。由于颗粒特定的润湿表面可能因被测技术而不同,所以直接测定的reff是有问题的,如气体吸收过程的测量。
通过使用一个粉末完美润湿的二次流体,上述提到的问题是可以克服的Diggins et al.(1990) and Diggins and Ralston (1993),对于接触角测量,他们的方法是:利用一个完美润湿液体即θ=0o,对比液体的润湿行为的程度。并且可以将这一步做为一个标准。而这项技术的要求是:基准液体的表面张力必须低于固体的临界润湿表面张力。环己烷(γ=25.5mN/m)是最常用的参比液体。基准液体的接触角θ2,等于零,因此就可以用它的毛细管压力来研究探测颗粒床层的几何形状。基于正确的选择参考液体,Prestidge and Ralston (1995)提出的方法获得成功。
值得注意的是,虽然这样的表面上得到的接触角通常不是杨氏接触角,但它是根据液体的表面张力,确定的拉普拉斯压力ΔP,毛细管渗透获得的一个确实存在的接触角。
Subrahmanyam等人(1999)对比了石英接触角的测量方法,即液体毛细管渗透法与捕收气泡技术,得出结论:在可浮性方面,毛细管渗透法比捕泡法具有更好的相关性。毛细管渗透法的优点在于它的操作简单、快捷,若要进行多次测量,则需要采取相应的改进,以提高可靠性。
实验过程中,此方法的主要挑战是在毛细管中获取一个常数和实现粉末的均质包装。这种方法的缺点是,由于后退接触角可以更好的与实际的浮选过程响应,所以后退接触角通常在浮选过程中引用,然而这种方法只可以获得前进接触角而不能获得后退接触角(Laskowski, 1994; Lam et al., 2002)。为了得到后退接触角,就必须克服实验困难并提出修改的方法,而这种方法的关键一步是,开发能够测量真正矿物表面接触角的装置。
4.结论
接触角测量技术,特别是那些适用于矿物表面的已被提出。为了快速获得表面的疏水特性,接触角测量技术已被广泛研究和应用在各种领域中。在矿物加工过程中,平坦矿物表面的测量技术相对于浮选过程中毛细管渗透方法是没有竞争力的。前一种方法的缺点是:为了获得一个矿物表面,实现最佳的测量而满足所有的实验条件是非常困难的。而对于杨-拉普拉斯方程来说的最佳适用性来说,异质性似乎是最大的问题。
通过分析可以得到的结论是,对于真实的矿物样品来说,颗粒毛细管渗透方法是最合适的接触角测量方法。而我们的目的也在于能够快速,准确,方便的获得真实矿物表面接触角的值。我们将来所要面临的挑战是,在颗粒大小,颗粒形状,非均质性,表面粗糙度,和表面活性剂等方面通过函数来量化接触角的值。一个新的强大的模型,需要理想与表观接触角之间所有参数之间的关系。如果在实际的系统中可以很容易的获得可靠的接触角测量数据,以及相关联的适当的浮选数据,那我们就可以利用这种测量从根本上研究颗粒的实际浮选行为。
5.感谢
向Dr. B. Follink, Mr. J.T. Woodcock and Mr. W.J. Bruckard of CSIRO Minerals在准备这篇稿子时提供的帮助表示感谢。
6.参考文献
Adamson, A.W., Gast, A.B., 1997. Physical Chemistry of Surfaces, sixth ed. JohnWiley & Sons, New York.
Bartell, F.E., Osterhof, H.J., 1927. Determination of the wettability of a solid by a liquid. Industrial and Engineering Chemistry 19 (11), 1277–1280
Bartell, F.E., Walton, C.W., 1934. Alteration of the surface properties of stibnite as revealed by adhesion tension studies. Journal of Physical Chemistry 38, 503–511.
Bartell, F.E., Whitney, C.E., 1932. Adhesion tension III. Journal of Physical Chemistry36, 3115–3126.
Bashforth, F., Adams, J.C., 1883. An Attempt to Test the Theory of Capillary Action.Cambridge University Press, Cambridge.
Bigelow, W.C., Pickett, D.L., Zisman, W.A., 1946. Oleophobic monolayers, I. Films adsorbed from solution in non-polar liquids. Journal of Colloid Science 1, 513–538.
Budziak, C.J., Neumann, A.W., 1990. Automation of the capillary rise technique for measuring contact angles. Colloids and Surfaces 43, 279–293.
Butt, H.-J., Graf, M., Kappl, M., 2006. Physics and Chemistry of Interfaces. Wiley-VCH, Weinheim.
Cheng, P., Li, D., Boruvka, L., Rotenberg, Y., Neumann, A.W., 1990. Automation of axisymmetric drop shape analysis for measurements of interfacial tensions and contact angles. Colloids and Surfaces 43 (2), 151–167.del Rio, O.I., Kwok, D.Y., Wu, R., Alvarez, J.M., Neumann, A.W., 1998. Contact angle measurements by axisymmetric drop shape analysis and an automated polynomial fit program. Colloids and Surfaces A: Physicochemical andEngineering Aspects 143, 197–210.
Diggins, D., Ralston, J., 1993. Particle wettability by equilibrium capillary pressure measurements. Coal Preparation 13, 1–19.
Diggins, D., Fokkink, L.G.J., Ralston, J., 1990. The wetting of angular quartz particles:capillary pressure and contact angles. Colloids and Surfaces 44, 299–313.
Ducker, W.A., Xu, Z., Israelachvili, J.N., 1994. Measurements of hydrophobic and DLVO forces in bubble–surface interactions in aqueous solutions. Langmuir 10,3279–3289.
Dunstan, D., White, L.R., 1986. A capillary pressure method for measurement of contact angles in powders and porous media. Journal of Colloid and Interface Science 111, 60–64.
Fisher, L.R., 1979. Measurement of small contact angles for sessile drops. Journal of Colloid and Interface Science 72, 200–205.
Fisher, L.R., Lark, P.D., 1979. An experimental study of the Washburn equation forliquid flow in very fine capillaries. Journal of Colloid and Interface Science 69,486–492.
Gaudin, A.M., 1957. Flotation, second ed.McGraw-Hill Book Company Inc.,NewYork.
Good, R.J., Lin, N.J., 1976. Rate of penetration of a fluid into a porous body: II verification of the generalization of the Washburn equation, for organic liquids in glass capillaries. Journal of Colloid and Interface Science 54, 52–58.
Hunter, R.J., 2001. Foundations of Colloid Science, second ed. Clarendon Press,Oxford.
Johnson, D.J., Miles, N.J., Hilal, N., 2006. Quantification of particle-bubble interactions using atomic force microscopy: a review. Advances in Colloid and Interface Science 127, 67–81.
Koh, P.T.L., Schwarz, M.P., 2003. CFD modelling of bubble–particle collision rates and efficiencies in a flotation cell. Minerals Engineering 16 (11), 1055–1059.
Koh, P.T.L., Schwarz, M.P., 2006. CFD modelling of bubble–particle attachments in flotation cells. Minerals Engineering 19 (6-8), 619–626.
Kwok, D.Y., Neumann, A.W., 1999. Contact angle techniques and measurements. In:
Milling, A.J. (Ed.), Surface Characterisation Methods: Priniples, Techniques and Applications. Marcel Dekker, New York, pp. 37–86.
Kwok, D.Y., Budziak, C.J., Neumann, A.W., 1995. Measurements of static and low rate dynamic contact angles by means of an automated capillary rise technique. Journal of Colloid and Interface Science 173, 143–150.
Kwok, D.Y., Lam, C.N.C., Li, A., Leung, A., Wu, R., Mok, E., Neumann, A.W., 1998. Measuring and interpreting contact angles: a complex issue. Colloids andSurfaces A: Physicochemical and Engineering Aspects 142, 219–235.
Lam, C.N.C., Wu, R., Li, D., Hair, M.L., Neumann, A.W., 2002. Study of the advancing and receding contact angles: liquid sorption as a cause of contact angle hysteresis. Advances in Colloid and Interface Science 96, 169–191.
Laskowski, J.S., 1994. Coal surface chemistry and its role in fine coal beneficiation and utilization. Coal Preparation 14 (3), 115–131.
Leja, J., and Poling, G.W., 1960. On the interpretation of contact angle. In: Proceedings of the 5th International Mineral Processing Congress IMM,London, pp. 325–332.
Levine, S., Lowndes, J., Watson, E.J., Neale, G., 1980. A theory of capillary rise of a liquid in a vertical cylindrical tube and in a parallel-plate channel: Washburn equation modified to account for the meniscus with slippage at the contact line.Journal of Colloid and Interface Science 73, 136–151.Marmur, A., 1996. Equilibrium contact angles: theory and measurement. Colloids and Surfaces A: Physicochemical and Engineering Aspects 116 (1–2), 55–61.
Mohammadi, R., Finlay, W.H., Roa, W., Amirfazli, A., 2003. Determination of contact angle of microspheres by microscopy methods. In: Proceedings of the International Conference on MEMS, NANO and Smart Systems, Banff Alberta,pp. 84–88.
Nguyen, A.V., Nalaskowski, J., Miller, J.D., 2003. The dynamic nature of contact angles as measured by atomic force microscopy. Journal of Colloid and Interface Science 262 (1), 303–306.
Prestidge, C.A., Ralston, J., 1995. Contact angle studies of galena particles. Journal of Colloid and Interface Science 172, 302–310.
Preuss, M., Butt, H.-J., 1999. Direct measurement of forces between particles and bubbles. International Journal of Mineral Processing 56, 99–115.
Ralston, J., Newcombe, G., 1992. Static and dynamic contact angles. In: Laskowski, J.,
Ralston, J. (Eds.), Colloid Chemistry in Mineral Processing. Elsevier Science Publishers, Amsterdam, pp. 194–201.
Ralston, J., Fornasiero, D., Hayes, R., 1999. Bubble–particle attachment and detachment in flotation. International Journal of Mineral Processing 56, 133–164.
Rodriguez-Valverde,M.A.,Cabrerizo-Vilchez,M.A.,Rosales-Lopez,P.,Paez-Duenas,A.,Hidalgo-Alvarez, R., 2002. Contact angle measurements on two (wood and stone) non-ideal surfaces. Colloids and Surfaces A: Physicochemical and Engineering Aspects 206 (1-3), 485–495.
Rotenberg, Y., Boruvka, L., Neumann, A.W., 1983. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces. Journal of Colloid and Interface Science 93, 169–183.
Spelt, J.K., Rotenberg, Y., Absolom, D.R., Neumann, A.W., 1987. Sessile–drop contact angle measurements using axisymmetric drop shape analysis. Colloids and Surfaces 24, 127–137.
Subrahmanyam, T.V., Monte, M.B.M., Middea, A., Valdiviezo, E., Lins, F.F., 1999. Contact angles of quartz by capillary penetration of liquids and captive bubble techniques. Minerals Engineering 12, 1347–1357.
Taggart, A.F., Taylor, T.C., Ince, C.R., 1930. Experiments with flotation agents.Transactions of the American Institute of Mining and Metallurgical Engineers 87, 285–386.
Tavana, H., Lam, C.N.C., Grundke, K., Friedel, P., Kwok, D.Y., Hair, M.L., Neumann,A.W., 2004. Contact angle measurements with liquids consisting of bulky molecules. Journal of Colloid and Interface Science 279, 493–502.
Wark, I.W., 1984. Contact angles and flotation research. In: Jones, M.H., Woodcock, J.T. (Eds.), Principles of Mineral Flotation, The Wark Symposium. The Australasian Institute of Mining and Metallurgy, Melbourne.
Wark, I.W., Cox, A.B., 1934. Principles of flotation. I. An experimental study of the effect of xanthates on contact angles at mineral surfaces. Transactions of the American Institute of Mining and Metallurgical Engineers 112, 189–244.
Washburn, E.W., 1921. The dynamics of capillary flow. Physical Review 17,273.
White, L.R., 1982. Capillary rise in powders. Journal of Colloid and Interface Science90, 536–538.
Wilhelmy, L., 1863. Annalen der Physik 119, 177.
